[Algorithm] Small Problems
고전 알고리즘 인 파이썬
Small problems
문제해결 방식에 대해 흥미로운 시각을 제시할 수 있는 작은 문제들을 살펴본다.
1.1 피보나치 수열
피보나치 수열은 첫째항을 0, 두번째 항을 1로 두고 그 다음의 항들은 직전 두 항의 합인 수열이다.
${0, 1, 1, 2, 3, 5, 8, 13, 21, \dots }$
$fib(0) = 0$
$fib(1) = 1$
$fib(n) = fib(n-1) + fib(n-2)$ $(n| {2,3,4,...}))$
1.1.1 재귀함수
1.1의 피보나치 수열을 재귀(recursion)방식을 통해 python function으로 구현한다.
#fib1
def fib1(n: int):
return fib1(n-1) + fib1(n-2)
fib1()에 값을 넣어 결과를 보면
print(fib1(5))
RecursionError: maximum recursion depth exceeded
재귀에러가 뜨며 fib1()이 결과를 return하지 않고 무한 재귀(infinite recursion)상태에 빠진다.
1.1.2 재귀함수와 기저조건
fib1()을 실행할 때까지 파이썬 인터프리터는 무한 재귀를 호출한다고 알려주지 않는다.
기저조건(base case): 재귀 함수에서 재귀함수를 탈출하는 조건이다.
#fib2
def fib2(n: int):
if n < 2: #기저 조건
return n
return fib2(n-2) + fib2(n-1) #재귀 조건
print(fib2(5))
print(fib2(10))
5
55
다만 fib2()함수에 50정도의 수만 넣어도 실행시간이 굉장히 길어질 것이다.
fib2()를 호출할 때마다 fib2(n-1)과 fib2(n-2)를 통해 호출트리가 기하급수적으로 커진다.
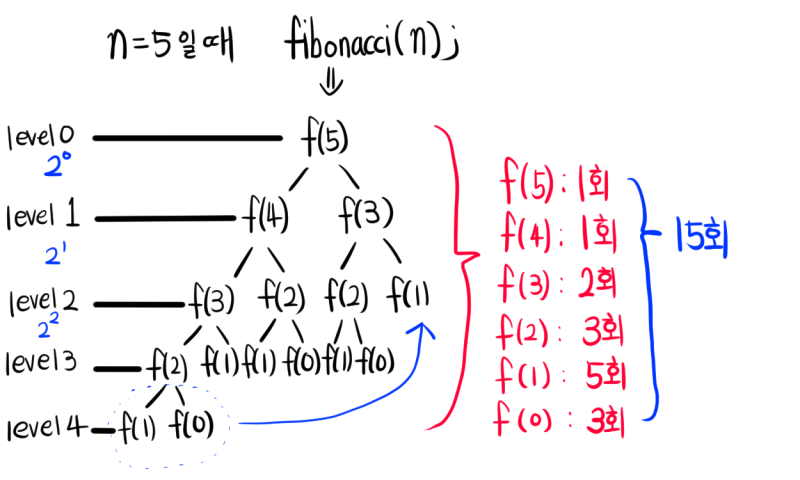
기저 조건에 해당하지 않는 모든 fib2() 호출은 fib2()를 2번 이상 호출한다.
import time
for n in range(30, 35, 1):
start = time.time() #시작 시간 측정
print(fib2(n))
print(f"fib2({n}) time :", time.time() - start)
832040
fib2(30) time : 0.25970911979675293
1346269
fib2(31) time : 0.4317185878753662
2178309
fib2(32) time : 0.6557610034942627
3524578
fib2(33) time : 1.1117711067199707
5702887
fib2(34) time : 1.7992608547210693
fib2()의 수열의 요소 숫자가 증가할 수록 함수 호출 증가 횟수는 더 악화된다.
fib2(5) => 15회 호출
fib2(10) => 177회 호출
fib2(20) => 21891회 호출
1.1.3 메모이제이션
메모이제이션은 계산 작업이 완료되면 결과를 저장하는 기술이다.
이전에 실행된 같은 계산을 수행할 때 다시 계산하지 않고 저장된 값을 사용한다.
#fib3
from typing import Dict
memo: Dict[int, int] = {0: 0, 1: 1} #기저 조건
def fib3(n: int):
if n not in memo:
memo[n] = fib3(n-1) + fib3(n-2)
return memo[n]
import time
start = time.time() #fib2의 시작 시간 측정
print(fib2(20))
print("fib2(20) time :", time.time() - start)
start = time.time() #fib3의 시작시간 측정
print(fib3(20))
print("fib3(20) time :", time.time() - start)
6765
fib2(20) time : 0.0019981861114501953
6765
fib3(20) time : 0.0
fib2(20)은 자신을 21,891번 호출하는 반면 fib3(20)은 39번을 호출한다.
1.1.4 메모이제이션 데커레이터
fib3()를 더 단순화할 수 있다. 파이썬에 모든 함수를 자동으로 메모이징하는 내장형 데커레이터@functools.lru_cache()를 사용하여 fib4()를 작성한다.
fib2()와 같은 코드를 사용하지만 fib4()가 실행될 때 마 데커레이터는 계산된 반환값을 메모리에 캐싱(저장)한다. 이후 동일한 인자와 fib4()가 실행되면 캐시된 값을 검색하여 반환한다.
#fib4
from functools import lru_cache
@lru_cache(maxsize = None)
def fib4(n: int):
if n < 2:
return n
return fib4(n-2) + fib4(n-1)
import time
start = time.time() #fib2의 시작 시간 측정
print(fib2(20))
print("fib2(20) time :", time.time() - start)
start = time.time() #fib4의 시작시간 측정
print(fib4(20))
print("fib4(20) time :", time.time() - start)
6765
fib2(20) time : 0.0020313262939453125
6765
fib4(20) time : 0.0
@lru_cache의 maxsize속성은 데커레이터 함수에서 가장 최근의 호출을 캐시할 수 있는 크기이다. None은 캐시에 제한이 없다는 것을 의미한다.
1.1.5 간단한 피보나치수열
고전적인 방식으로 피보나치 수열을 풀어보면
#fib5
def fib5(n: int):
if n == 0: return n
last: int = 0 #fib(0)
next: int = 1 #fib(1)
for _ in range(1, n):
last, next = next, last + next
return next
import time
start = time.time() #fib2의 시작 시간 측정
print(fib2(20))
print("fib2(20) time :", time.time() - start)
start = time.time() #fib5의 시작시간 측정
print(fib5(20))
print("fib5(20) time :", time.time() - start)
6765
fib2(20) time : 0.0019998550415039062
6765
fib5(20) time : 0.0
fib5()의 for문은 튜플 언패킹(tuple unpacking) 을 사용했다.
변수 last는 변수 next의 이전값으로 갱신되고
변수 next는 last의 이전 값 + next의 이전값 으로 설정된다.
즉 변수
last가 갱신된 후 변수next가 전에 변수next의 이전 값을 저장할 임시 변수를 만들지 않아 메모리를 절약할 수 있다.
변수를 swap할 때 튜플 언패킹을 사용하는 것은 파이썬에서 일반적이다.
fib5()는 피보나치 수열을 구하는 가장 효율적인 방법으로 for 문이 최대 n-1회 실행된다.
fib5(20)은 19회 순회한다.
단순 재귀의 경우 상향식(bottom-up)방식으로 계산한다. fib5()의 경우 하향식(top-down)방식으로 계산한다.
fib1(), fib2()처럼 때론 재귀가 문제를 해결하는 가장 직관적인 방법이지만 성능에 문제가 일어날 수 있다.
1.1.6 제너레이터와 피보나치 수
피보나치 수열의 해당 단일값까지 전체 수열을 구하려면 yield 문을 사용하여 fib5()를 파이썬 제너레이터로 쉽게 변환할 수 있다.
Generator 참고문헌
#fib6
from typing import Generator
def fib6(n: int) -> Generator[int, None, None]:
yield 0 #특수 조건 fib(0)
if n > 0: yield 1 #특수 조건 fib(1)
last: int = 0 #fib(0)
next: int = 1 #fib(1)
for _ in range(1, n):
last, next = next, last+next
yield next #제너레이터 핵심 반환문
count = 0
for i in fib6(50):
print(f"fib6({count}) = {i}\t", end='')
count += 1
fib6(0) = 0 fib6(1) = 1 fib6(2) = 1 fib6(3) = 2 fib6(4) = 3 fib6(5) = 5 fib6(6) = 8 fib6(7) = 13 fib6(8) = 21 fib6(9) = 34 fib6(10) = 55 fib6(11) = 89 fib6(12) = 144 fib6(13) = 233 fib6(14) = 377 fib6(15) = 610 fib6(16) = 987 fib6(17) = 1597 fib6(18) = 2584 fib6(19) = 4181 fib6(20) = 6765 fib6(21) = 10946 fib6(22) = 17711 fib6(23) = 28657 fib6(24) = 46368 fib6(25) = 75025 fib6(26) = 121393 fib6(27) = 196418 fib6(28) = 317811 fib6(29) = 514229 fib6(30) = 832040 fib6(31) = 1346269 fib6(32) = 2178309 fib6(33) = 3524578 fib6(34) = 5702887 fib6(35) = 9227465 fib6(36) = 14930352 fib6(37) = 24157817 fib6(38) = 39088169 fib6(39) = 63245986 fib6(40) = 102334155 fib6(41) = 165580141 fib6(42) = 267914296 fib6(43) = 433494437 fib6(44) = 701408733 fib6(45) = 1134903170 fib6(46) = 1836311903 fib6(47) = 2971215073 fib6(48) = 4807526976 fib6(49) = 7778742049 fib6(50) = 12586269025
fib6(50)을 실행하면 피보나치 수열의 51개 숫자가 출력되며 for i in fib6(50):에서 매 반복마다 fib6()의 yield문이 실행된다.
만약 fib6(50)의 끝에 도달하여 더 이상 반환될 yield가 없다면 for문은 반복을 종료한다.
1.2 압축 알고리즘
저장공간(가상메모리 or 메인메모리)을 절약하는 것은 중요하다. 더 적은 공간을 사용하는 것이 효율적이며, 경제적인 것은 당연하다.
Compression 은 더 적은 저장공간을 사용하도록 데이터의 형태를 변형시켜 사용하는 것이다.
반대로 Decompression 은 compression의 프로세스를 반대로 행하는 것이며 데이터의 형태를 원래대로 복구하는 것이다.
CAUTION: Compression , Decompression 과정에서 시간이 걸리기 때문에 처리시간과 저장공간은 tadeoff의 관계를 가진다.
그러므로 압축알고리즘은 아래와 같은 상황에서 주로 사용된다.
- 빠른 실행시간이 상대적으로 덜 중요한 작은 규모의 상황
- 인터넷을 통해 큰 규모의 데이터를 전송해야 할 때
- 서버에 저장될 때
가장 쉬운 저장공간의 절약으로는 자료형을 명시하는 방법이 있다.
| 자료형 | 크기(byte) | 수의 표현 범위 |
|---|---|---|
| char | 1 | $-2^7$ ~ $2^7 - 1$ (-128 ~ 127) |
| signed char | 1 | $-2^7$ ~ $2^7 - 1$ (-128 ~ 127) |
| unsigned char | 1 | 0 ~ $2^8 - 1$ (0 ~ 255) |
| short int | 2 | $-2^15$ ~ $2^15 - 1$ (-32,768 ~ 32,767) |
| unsinged short int | 2 | 0 ~ $2^16$ (0 ~ 65,535) |
| int | 4 | $-2^31$ ~ $2^31 - 1$ (-2,147,483,648 ~ 2,147,483,647) |
| unsigned int | 4 | 0 ~ $2^32 -1$ (0 ~ 4,294,967,295) |
| long int | 4 | $-2^31$ ~ $2^31 - 1$ (-2,147,483,648 ~ 2,147,483,647) |
| unsigned long int | 4 | 0 ~ $2^32 -1$ (0 ~ 4,294,967,295) |
| float | 4 | $-10^128$ ~ $10^127$ : 소수 6자리 표현 |
| double | 8 | $-10^128$ ~ $10^127$ : 소수 15자리 표현 |
| long double | 8 이상 | double의 정밀도와 같거나 크다 |
하지만 파이썬의 경우 부호없는 자료형이 지원되지 않는다. python object system에서 28byte 이하의 int 자료형은 만들 수 없으며 초과시에 1bit씩 증가한다.
DNA는 Adenine, Thymine, Cytosine, Guanine의 조합으로 이루어져있다. 순서를 str 자료형으로 저장하게 되면 24bit의 저장공간을 차지하지만 2진수로 변환하여 저장하면 6bit의 저장공간을 차지한다.
'ATG'(24bit) = 'A'(8bit) + 'T'(8bit) + 'G'(8bit) '001110'(6bit) = '00'(2bit) + '11'(2bit) + '10'(2bit)
아래 trival_compression은 str (‘A’, ‘C’, ‘G’, ‘T’)를 int (‘00’, ‘01’, ‘10’, ‘11’)로 변환하는 코드이다.
# trival_compression.py
class CompressedGene:
def __init__(self, gene: str) -> None: # str형의 자료가 들어오면 _compress()함수 호출
self._compress(gene)
def _compress(self, gene: str) -> None:
self.bit_string: int = 1
for nucleotide in gene.upper():
self.bit_string <<= 2 # 좌측으로 2bit shift
if nucleotide == 'A': # 마지막 2bit -> 00
self.bit_string |= 0b00
elif nucleotide == 'C': # 마지막 2bit -> 01
self.bit_string |= 0b01
elif nucleotide == 'G': # 마지막 2bit -> 10
self.bit_string |= 0b10
elif nucleotide == 'T': # 마지막 2bit -> 11
self.bit_string |= 0b11
else:
raise ValueError(f"Invalid Nucleotide: {nucleotide}")
def decompress(self) -> str:
gene: str = ""
for i in range(0, self.bit_string.bit_length() -1, 2):
bits: int = self.bit_string >> i & 0b11 #2bit씩 get
if bits == 0b00: #A
gene += "A"
elif bits == 0b01: #C
gene += "C"
elif bits == 0b10: #G
gene += "G"
elif bits == 0b11: #T
gene += "T"
else:
raise ValueError(f"Invalid bits: {bits}")
return gene[::-1] #백워드 슬라이싱을 통해 reverse
def __str__(self):
return self.decompress()
_compress()는 str자료형의 nucleotides를 int 자료형으로 변환한다.
A -> 00 C -> 01 G -> 10 T -> 11
좌측 시프트 연산으로 우측 두 비트를 00으로 세트한 후
or연산을 통해 원하는 비트로 세트한다.
self.bit_string |= 0b00
decompress()는 int자료형의 2개의 비트를 str자료형의 nucleotides로 변환한다.
우측 시프트 연산과 00과의 and연산을 통해 뒤에서부터 2개의 비트를 얻어와 매칭되는 nucleotides로 변환한 후 슬라이싱을 이용한 reverse한 str을 반환한다.
from sys import getsizeof
original: str = \
"TAGGGATTAACCGTTATATATATATAGCCATGGATCGATTATATAGGGATTAACCGTTATATATATATAGCCATGGATCGATTATA" * 100
print(f"original is {getsizeof(original)} bytes")
compressed: CompressedGene = CompressedGene(original) # compress
print(f"compressed is {getsizeof(compressed.bit_string)} bytes")
print(compressed) # decompress
print(f"original and decompressed are the same: {original == compressed.decompress()}")
original is 8649 bytes
compressed is 2320 bytes
TAGGGATTAACCGTTATATATATATAGCCATGG ... GATTAACCGTTATATATATATAGCCATGGATCGATTATA
original and decompressed are the same: True
_compress()를 통해 저장공간을 75%를 절약할 수 있다.
1.3 깨지지않는 암호화
one-time pad 는 기존 데이터의 일부와 의미없는 더미데이터를 병합하여 암호화하여 더미 키와 product키를 만드는 암호화 기법이다.
암호화된 product와 더미데이터 모두 접근을 하지 못하면 기존 데이터를 복원하는 것은 불가능하다.
1.3.1 데이터 순서 대로 가져오기
one-time pad 암호화를 사용하여 문자열을 암호화 할 경우, Python3의 str은 UTF-8 bytes(Unicode character encoding)의 시퀀스를 생각해야 한다.
str은 encode()하여 UTF-8 bytes의 시퀀스로 변환되며 반대로 UTF-8 bytes는 decode()하여 str로 변환된다.
one-time pad 암호화에 사용되는 dummy data의 3가지 원칙
- dummy data와의 결합으로 생기는 product는 깨지지않아야한다.
- dummy data는 original data와 같은 길이여야 한다.
- dummy data는 완전 랜덤이며 비밀이어야 한다.
dummy data가 짧은 주기로 반복되거나 다른곳에서 주기적으로 사용된어 패턴이 관찰된다면 attacker에 의해 깨질 수 있다.
아래의 코드는 secrets 모듈의 token_bytes() 를 통해 유사난수를 생성해 사용한다.
NOTE: secrets 패키지의 난수발생 제너레이터를 사용하기 때문에 발생하는 유사난수는 완전히 랜덤하지는 않다. 그러나 목적에 충분히 가깝기 때문에 dummy data로 사용한다.
# unbreakable_encryption.py
from secrets import token_bytes
from typing import Tuple
def random_key(length: int) -> int:
#length 길이의 랜덤 bytes 발생
tb: bytes = token_bytes(length)
#발생한 랜덤 bytes를 bit string으로 변환
return int.from_bytes(tb, "big")
from_bytes()랜덤으로 발생한 bytes » int
예시.7bytes (7 bytes * 8 bits = 56 bits)56 bits의 int로 변환
1.3.2 암호화와 복호화
unbreakable_encryption 을 통해 만들어진 dummy data와 original data를 암호화 하는 방법은 XOR연산을 이용한다.
| A | B | A^B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
original_key ^ dummy = product product ^ dummy = original_key product ^ original_key = dummy
original data와 dummy data의 XOR 연산을 통해 product와 dummy를 return 한다
# unbreakable_encryption.py
def encrypt(original: str) -> Tuple[int, int]:
original_bytes: bytes = original.encode()
dummy: int = random_key(len(original_bytes))
original_key: int = int.from_bytes(original_bytes, "big")
encrypted: int = original_key ^ dummy # XOR 연산
return dummy, encrypted
NOTE: int.from_bytes 의 2가지 인수는 int로 변환할 bytes와 big 은 엔디안 컴퓨터가 bytes를 정렬하는 순서를 의미한다. unbreakable_encryption 의 경우 bit 단위의 데이터만 조작하기 때문에 순서가 상관없지만, 다른 encoding과정에서는 순서가 중요할 수도 있다.
복호화도 마찬가지로 XOR 연산을 사용하며, 두 key(dummy, encrypted)를 사용하여 original: str로 변환한다.
int.to_bytes() int » bytes
def decrypt(key1: int, key2: int) -> str:
decrypted: int = key1 ^ key2 #XOR 연산
temp: bytes = decrypted.to_bytes((decrypted.bit_length() + 7) // 8, "big")
return temp.decode()
bit 길이에 7을 더하는 이유는 8로 나누기 전 반올림하여 off-by-one error를 피하기 위함이다.
key1, key2 = encrypt("One Time Pad!")
result: str = decrypt(key1, key2)
print(result)
One Time Pad!
1.4 파이 계산하기
수학적으로 $\pi$를 유도하는 공식으로는 라이프니츠 공식이 있다. 다음의 무한급수는 $\pi$에 수렴한다고 가정한다.
$\pi$ = $\frac{4}{1}$ - $\frac{4}{3}$ + $\frac{4}{5}$ - $\frac{4}{7}$ + $\frac{4}{9}$ - $\frac{4}{11} \dots$
#calculating_pi.py
def calculate_pi(n_terms: int) -> float:
numerator: float = 4.0 #분자
denominator: float = 1.0 #분모
operation: float = 1.0 #연산(덧셈, 뺄셈)
pi: float = 0.0
for _ in range(n_terms):
pi += operation * (numerator/denominator)
denominator += 2.0
operation *= -1.0
return pi
print(calculate_pi(1000000))
3.1415916535897743
Tip: 대부분의 플렛폼과 같이 Python 의 float자료형은 64bit 부동소수점 수(== double in C)
calculating_pi 함수는 수식과 프로그래밍 코드간의 기계적인 변환을 보여주는 모델인 것에 의미를 가진다. 하지만 가장 효율적인 솔루션은 아님을 명심해야한다.
1.5 하노이의 탑
하노이의 탑은 세개의 기둥(A,B,C 라고 명시)에 있는 다양한 크기의 디스크를 다른 기둥으로 옮기는 게임으로 아래의 규칙을 따른다.
- 한번에 하나의 디스크만 옮길 수 있다.
- 가장 위에 있는 디스크만 옮길 수 있다.
- 디스크 위에는 더 작은 디스크만이 올라갈 수 있다.

https://shoark7.github.io/programming/algorithm/tower-of-hanoi
1.5.1 하노이의 탑 모델링
stack 구조를 통해 모델링한다. stack구조는 Last-In-First-Out(LIFO)의 방식을 따르는 자료구조이다.
stack 의 주된 메소드
- push() : stack에 자료를 저장
- pop() : 가장 최근에 저장된 자료를 뺌
Python의 List 자료형을 통해 쉽게 구현가능하다.
# stack
from typing import TypeVar, Generic, List
T = TypeVar('T')
class Stack(Generic[T]):
def __init__(self) -> None:
self._container: List[T] = []
def push(self, item: T) -> None:
self._container.append(item)
def pop(self) -> T:
return self._container.pop()
def __repr__(self) -> str:
return repr(self._container)
Note: 임의의 유형 T는 T = TypeVar('T') 에 의해 정의되어있으며, T는 어떤 타입도 될 수 있다. 하노이의 탑 문제를 해결하기 위해 Stack[int] 타입으로 채워진다. 이는 ‘T’가 int타입으로 채워진다는 것을 의미한다.
Stack 구조의 탑 tower_a 에 discs 3개를 push() 한다.
#A타워에 디스크 넣기
num_discs: int = 3
tower_a: Stack[int] = Stack()
tower_b: Stack[int] = Stack()
tower_c: Stack[int] = Stack()
for i in range(1, num_discs+1): # 1, 2, 3
tower_a.push(i)
1.5.2 하노이의 탑 해결
하나의 디스크를 이동시키는 것은 재귀함수를 통해 해결할 수 있다. 하지만 핵심은 하나의 디스크 사례와 다수의 디스크 사례를 해결하는 시나리오를 코드화 시켜야한다는 것이다.
tower_a 에서 tower_c로 n개의 디스크를 이동시켜야 할 때
- 맨 아래에 위치한 디스크를 제외한 n-1개의 디스크를
tower_a >> tower_b옮긴다. - 가장 아래에 위치한 디스크를
tower_a >> tower_c로 옮긴다. tower_b >> tower_c로 n-1개의 디스크를 이동시킨다.
재귀알고리즘을 통해 구현하면 디스크의 개수에 상관없이 작동하는 알고리즘을 만들 수 있다.
#hanoi
def hanoi(begin: Stack[int], end: Stack[int], temp: Stack[int], n: int) -> None:
if n == 1: #기저조건
end.push(begin.pop())
else:
hanoi(begin, temp, end, n-1) # 1: n-1개의 discs tower_a->tower_b
hanoi(begin, end, temp, 1) # 2: 가장 아래의 disc tower_a->tower_c
hanoi(temp, end, begin, n-1) # 3: 1번의 n-1개 discs tower_b->tower_c
print(f"이동 전 A: {tower_a} B: {tower_b} C: {tower_b}")
hanoi(tower_a, tower_c, tower_b, num_discs)
print(f"이동 후 A: {tower_a} B: {tower_b} C: {tower_c}")
이동 전 A: [1, 2, 3] B: [] C: []
이동 후 A: [] B: [] C: [1, 2, 3]
재귀알고리즘을 사용하면 각 단계에서 discs가 어떻게 이동하는지 알 필요없이 추상적인 생각만으로 알고리즘을 구현할 수 있다.
Note: 일반적으로 원판이 n개 일 때, $2^n$−1번의 이동으로 원판을 모두 옮길 수 있다. 참고로 64개의 원판을 옮기는 데 총 $2^{64}$−1번 원판을 움직여야 하고, 1초에 하나의 원판을 옮긴다고 가정했을 때 5,849억년 정도 걸린다.
이것은 tutle 패키지을 이용해 시각화한 자료이다.
1.6 적용사례
recursion
많은 알고리즘, 프로그래밍 언어의 핵심이며 Scheme, Haskell 등의 함수형 프로그래밍 언어에서 반복문을 대체한다. 그러나 재귀기술을 사용한 알고리즘은 반복문을 통해서도 이룰 수 있다.
Meomoization
메모이제이션은 파서(언어해석 프로그램)의 작업속도를 높일 수 있으며, 최근 계산의 결과가 다시 사용되는 모든 프로그램에서 유용한다.
Compression
압축은 대역폭의 영향을 받는 인터넷 연결에서 유용하게 사용되며 대부분의 압축알고리즘은 반복되는 정보를 제거할 수 있는 데이터 세트 내 구조나 패턴을 찾는 방식으로 사용된다.
One-time pad
암호화 복호화를 하기 위해 더미 키를 알아야 하고 또한 키를 비밀로 유지하는 암호화 체계를 반하기 때문에 일반적인 암호화에 실용적이지는 않다.
1.7 연습문제
1.
행렬을 이용한 피보나치 수열 n번째 피보나치 수열을 $F_n$ 이라고 할 때
$\begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1}\ \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0\ \end{pmatrix}^n$
$F_{(0,1)}$, $F_{(1,1)}$ 이 $F_n$이 된다.
분할정복 기법으로 잘게 나눈 후, 나눠진 값을 더해서 최종값을 구할 수 있다.
10번째 피보나치 수열을 분할 정복 기법으로 풀게 되면
분할
-
$\begin{pmatrix} F_{10+1} & F_{10} \\ F_{10} & F_{10-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^\frac{10}{2} \times \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^\frac{10}{2}$
-
$\begin{pmatrix} F_{5+1} & F_{5} \\ F_{5} & F_{5-1}\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^{5-1} \times \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}$
-
$\begin{pmatrix} F_{4+1} & F_{4} \\ F_{4} & F_{4-1}\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^\frac{4}{2} \times \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^\frac{4}{2}$
-
$\begin{pmatrix} F_{2+1} & F_{2} \\ F_{2} & F_{2-1}\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \times \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}$
이후 거꾸로 계산하여 합하여 정복한다.
# 두 행렬의 곱을 구한다
def matrix_mul(a, b):
temp = [[0] * 2 for _ in range(2)]
for i in range(2):
for j in range(2):
for k in range(2):
temp[i][j] += (a[i][k] * b[k][j])
return temp
# 분할
def matrix_pow(n, M):
if n == 1:
return M
if n % 2 == 0: #n이 짝수일 경우 n//2로 분할
temp = matrix_pow(n//2, M)
return matrix_mul(temp, temp)
else: #n이 홀수일 경우 n-1, BASE로 분할
temp = matrix_pow(n-1, M)
return matrix_mul(temp, M)
def fib(n):
BASE = [[1,1],[1,0]]
return (matrix_pow(n, BASE)[1][0])
print(fib(10))
55
1.1 피보나치 수열 알고리즘은 최대 n-1회 수행함으로 시간복잡도는 O(n)이지만 fib() 함수는 분할 정복 기법을 사용하여 시간복잡도는 O($\log_2 n$) 이다.
참고문헌

고전 알고리즘 인 파이썬
Leave a comment