[Algorithm] 검색 문제
고전 알고리즘 인 파이썬
2.1 DNA 검색
유전자는 A, C, G, T의 문자 시퀀스로 표현하며, 각 문자는 nucleotide 를 나타내고, 세 개의 뉴클레오타이드의 조합을 codon 이라고 한다. 특정 아미노산에 대한 코돈 코드는 다른 아미노산과 함께 단백질을 형성 할 수 있다.
2.1.1 DNA 정렬
4개의 뉴클레오타이드 (A, C, G, T)를 IntEnum 으로 나타낼 수 있다.
# dna_search.py
from enum import IntEnum
from typing import Tuple, List
Nucleotide: IntEnum = IntEnum('Nucleotide', ('A','C','G','T'))
Enum대신에IntEnum을 사용하는 이유는 비교연산자 (>, <, =..등)을 사용할 수 있기 때문이다.
이런 데이터 타입은 구현하려는 검색 알고리즘에서 작동할 수 있어야 하기 때문에Tuple과List를 사용한다.
코돈은 3개의 뉴클레오타이드를 Tuple 로 정의한다.
# dna_search.py
...
Codon = Tuple[Nucleotide, Nucleotide, Nucleotide] # 코돈 타입 앨리어스
Gene = List[Codon] # 유전자 타입 앨리어스
NOTE: 파이썬은 비슷한 타입으로 구성된 튜플 간의 비교를 기본적으로 지원하기 때문에 코돈을 비교할 < 연산자로 사용자 정의 클래스를 정의할 필요가 없다.
일반적으로 유전자는 유전자 내부의 모든 뉴클레오타이드를 나열한 문자열을 포함하는 파일 형식일 것이다.
코드에서는 가상의 유전자에 대해 그러한 문자열을 gene_str 로 선언한다.
# dna_search.py 계속
...
gene_str: str = "ACGTGGCTCTCTAACGTACGTACGTACGGGGTTTATATATACCCTAGGACTCCCTTT"
# 문자열을 Gene 타입으로 변환하는 함수
def string_to_gene(s: str) -> Gene:
gene: Gene = []
for i in range(0, len(s), 3):
if (i+2) >= len(s): # 3개의 뉴클레오타이드를 묶을 수 없으면 실행하지 않는다.
return gene
# 3개의 뉴클레오타이드를 통해 코돈 생성
codon: Codon = (Nucleotide[s[i]], Nucleotide[s[i + 1]], Nucleotide[s[i + 2]])
gene.append(codon) # 코돈을 유전자에 추가
return gene
my_gene: Gene = string_to_gene(gene_str)
string_to_gene() 함수는 문자열을 취해 세 개의 문자를 코돈(codon)으로 변환하여 새 리스트 유전자 Gene 끝에 추가한다.
3개의 뉴클레오타이드로 묶을 수 없다면 불완전한 유전자의 끝에 도달했다는 것으로, 하나 또는 두 개의 뉴클레오타이드를 건너뛴다.
2.1.2 선형 검색
유전자에서 특정 코돈이 존재하는지 여부를 검색한다.
선형 검색 은 찾고자 하는 요소를 발견하거나 자료구조의 끝에 도달할 때까지 순서대로 모든 요소를 확인하는 검색으로 가장 간단한 방법이다.
선형 검색의 시간복잡도는 아래 표와 같다.
| 최선 | 최악 | 평균 | |
|---|---|---|---|
| 항목에 존재할 경우 | 1 | n | $\frac{n}{2}$ |
| 항목에 존재하지 않을 경우 | n | n | n |
단순히 자료구조의 모든 요소를 탐색하면서 탐색할 항목과 동등한지 확인한다. 다음 코드는 유전자에서 특정 코돈이 존재하는 지 찾는 선형 검색 함수이다.
# dna_search.py
...
def linear_contains(gene: Gene, key_codon: Codon) -> bool:
for codon in gene:
if codon == key_codon:
return True
return False
acg: Codon = (Nucleotide.A, Nucleotide.C, Nucleotide.G)
gat: Codon = (Nucleotide.G, Nucleotide.A, Nucleotide.T)
print(linear_contains(my_gene, acg)) # True
print(linear_contains(my_gene, gat)) # False
True
False
NOTE: 파이썬 내장 시퀀스 타입(List, Tuple, range)은 모두 __contains__() 특수 메서드를 구현해, in 연산자를 통해 특정 항목을 검색할 수 있다. 실제로 in 연산자는 __contains__() 메서드를 구현하는 모든 타입과 함께 사용할 수 있다. my_gene 변수에서 acg 변수를 검색한 뒤 print(acg in my_gene) 함수로 결과를 출력할 수 있다.
print(acg in my_gene) # True
True
2.1.3 이진 검색
이진 검색(binary search)는 선형 검색보다 빠른 검색이지만, 해당 자료구조의 저장 순서를 미리 알고 있어야 한다. 자료구조가 정렬되어 있고, 그 인덱스로 항목에 즉시 접근할 수 있는 경우 이진 검색을 할 수 있다.
사전 순 으로 정렬된 단어의 리스트 ["cat", "dog", "kangaroo", "llama", "rabbit", "rat", "zebra"]에서 'rat'을 찾는다.
이진 검색의 과정
- 7개의 항목 중 중간요소는
'llama'이다. - 찾고자 하는
'rat'의 알파벳 순서가'llama'다음이므로 검색 범위를 중간 이후 리스트로 줄인다. 이 단계에서'rat'을 발견했다면 해당 인덱스를 반환하고 만약'rat'이 중간 요소의 알파벳순서보다 앞에 있다면 중간 이전 리스트로 줄인다. - 반으로 줄어든 범위의 리스트를 대상으로 1번과 2번과정을 다시 수행한다. 이 단계는 찾고자 하는 요소를 발견하거나 줄여진 리스트에 검색요소가 없을 때까지 계속 실행한다.
| 비교횟수 | 탐색구간의 크기 |
|---|---|
| 1 | $\frac{n}{2}$ |
| 2 | $\frac{n}{4}$ |
| 3 | $\frac{n}{8}$ |
| $\vdots$ | $\vdots$ |
| k | $\frac{n}{2^k}$ |
이진 검색은 검색 공간을 계속해서 절반으로 줄이므로 최악의 시간복잡도는 $O(\log_2 n)$이다.
그러나 선형 검색과 달리 정렬된 자료구조가 필요하며, 그렇지 않다면 정렬에 시간이 소요된다. 최적의 정렬 알고리즘의 시간복잡도는 O($n\log_2 n$)이므로, 검색을 한 번만 수행하려 한다면 선형 검색이 좋을 수 있다.
검색이 여러 번 수행된다면 이진 검색이 더 효율적일 것이다.
# dna_search.py
# 유전자와 코돈에 대한 이진 검색 함수
...
def binary_contains(gene: Gene, key_codon: Codon) -> bool:
low: int = 0
high: int = len(gene) - 1 # 자료구조 마지막 인덱스
while low <= high: # 검색 공간이 있다면 수행
mid: int = (low + high) // 2
if gene[mid] < key_codon: # 검색할 요소가 중간요소 뒤에 위치
low = mid + 1
elif gene[mid] > key_codon: # 검색할 요소가 중간요소 앞에 위치
high = mid - 1
else:
return True
return False
my_sorted_gene: Gene = sorted(my_gene)
print(binary_contains(my_sorted_gene, acg)) # true
print(binary_contains(my_sorted_gene, gat)) # false
True
False
2.1.4 제네릭 검색
linear_contains() 와 binary_contains() 함수는 파이썬의 거의 모든 시퀀스에서 동작하도록 일반화 할 수 있다.
NOTE: 아래 코드를 실행하기 전에 파이썬 3.7 이전 버전에서는 typing_extensions 모듈을 설치해야 한다. 파이썬 인터프리터 구성에 따라 다음과 같이 설치한다.
프로토콜 타입에 접근하려면 위의 모듈이 필요하며 파이썬 3.8 버전 이후에는 typing_extensions 모듈을 설치할 필요가 없으며,
from typing import Protocol을 사용하면 된다.
- $pip install typing_extensions
또는
- $pip3 install typing_extensions
#generic_search.py
from __future__ import annotations
from typing import TypeVar, Iterable, Sequence, Generic, List, Callable, Set, Deque, Dict, Any, Optional
from typing_extensions import Protocol
from heapq import heappush, heappop
T = TypeVar('T')
def linear_contains(iterable: Iterable[T], key: T) -> bool:
for item in iterable:
if item == key:
return True
return False
C = TypeVar('C', bound = "Comparable")
class Comparable(Protocol):
def __eq__(self, other: Any) -> bool:
return self == other
def __lt__(self: C, other: C) -> bool:
return not (self > other) and self != other
def __gt__(self: C, other: C) -> bool:
return (not self < other) and self != other
def __le__(self: C, other: C) -> bool:
return self < other or self == other
def __ge__(self: C, other: C) -> bool:
return not self < other
def binary_contains(sequence: Sequence[C], key: C) -> bool:
low: int = 0
high: int = len(sequence) - 1
while low <= high: # 검색 공간이 존재
mid: int = (low + high) // 2
if sequence[mid] < key:
low = mid + 1
elif sequence[mid] > key:
high = mid - 1
else:
return True
return False
print(linear_contains([1,5,15,15,15,15,20], 5)) #true
print(binary_contains(["a","d","e","f","z"], "f")) #true
print(binary_contains(["john","mark","ronald","sarah"],"sheila")) #false
True
True
False
일반화된 코드를 사용하여 거의 모든 컬렉션에서 데이터 타입과 상관없이 사용가능하다.
2.2 미로 찾기
미로의 경로를 문자를 이용해서 찾고 너비 우선 탐색, 깊이 우선 탐색, $A^*$ 알고리즘을 구현한다.
#maze.py
from enum import Enum
from typing import List, NamedTuple, Callable, Optional
import random
from math import sqrt
from generic_search import dfs, bfs, node_to_path, astar, Node
class Cell(str, Enum):
EMPTY = " "
BLOCKED = "X"
START = "S"
GOAL = "G"
PATH = "*"
class MazeLocation(NamedTuple):
row: int
column: int
from generic_search 는 아래에서 정의한다.
미로의 개별 위치를 나타내느 방법으로 행과 열 속성을 가진 네임드튜플(NamedTuple)을 사용한다.
2.2.1 미로 무작위로 생성하기
Maze 클래스는 상태를 나타내는 격자 (리스트의 리스트)를 내부적으로 추적한다. 행 수, 열 수, 시작 위치 및 목표 위치에 대한 인스턴스 변수를 가지고 있다. 격자에는 막힌 공간이 무작위로 채워진다.
START 에서 GOAL 까지 항상 경로가 존재해야 함으로 BLOCKED의 무작위 생성비율을 조정한다.
매개변수의 기본값(임곗값)은 20%이다(sparseness: float = 0.2). 무작위로 생성된 값이 sparseness 파라미터의 임곗값보다 더 작을 경우 공간은 벽으로 채워진다.
#maze.py
class Maze:
def __init__(self, rows: int = 10, columns: int = 10,
sparseness: float = 0.2,
start: MazeLocation = MazeLocation(0,0),
goal: MazeLocation= MazeLocation(9,9)) -> None:
#기본 인스턴스 변수 초기화
self._rows: int = rows
self._columns: int = columns
self.start: MazeLocation = start
self.goal: MazeLocation = goal
# 격자를 빈 공간으로 채운다.
self._grid: List[List[Cell]] = [[Cell.EMPTY for c in range(columns)] for r in range(rows)]
# 격자에 막힌 공간을 무작위로 채운다.
self._randomly_fill(rows, columns, sparseness)
# 시작 위치와 목표 위치를 설정
self._grid[start.row][start.column] = Cell.START
self._grid[goal.row][goal.column] = Cell.GOAL
def _randomly_fill(self, rows: int, columns: int, sparseness: float):
for row in range(rows):
for column in range(columns):
if random.uniform(0, 1.0) < sparseness:
self._grid[row][column] = Cell.BLOCKED
def __str__(self) -> str:
output: str = ""
for row in self._grid:
output += "".join([c.value for c in row]) + "\n"
return output
def goal_test(self, ml: MazeLocation) -> bool: # 목표지점에 도달했는지 검사
return ml == self.goal
def successors(self, ml: MazeLocation) -> List[MazeLocation]:
locations: List[MazeLocation] = []
if ml.row + 1 < self._rows and self._grid[ml.row + 1][ml.column] != Cell.BLOCKED: # 하측 이동 가능
locations.append(MazeLocation(ml.row + 1, ml.column))
if ml.row - 1 >= 0 and self._grid[ml.row - 1][ml.column] != Cell.BLOCKED: # 상측 이동 가능
locations.append(MazeLocation(ml.row - 1, ml.column))
if ml.column + 1 < self._columns and self._grid[ml.row][ml.column + 1] != Cell.BLOCKED: # 우측 이동 가능
locations.append(MazeLocation(ml.row, ml.column + 1))
if ml.column - 1 >= 0 and self._grid[ml.row][ml.column - 1] != Cell.BLOCKED: # 좌측 이동 가능
locations.append(MazeLocation(ml.row, ml.column - 1))
return locations
maze: Maze = Maze()
print(maze)
S
X
X X X X
X X
X
X
X
X
X XG
2.2.2 미로 세부사항
goal_test() 는 미로에서 길을 찾는 동안 목표 지점에 도달했는지 여부를 확인한다.
검색된 특정 위치(MazeLocation 네임드튜플)가 목표 지점인지 확인하여 bool 자료형으로 반환한다.
successors() 메서드는 주어진 미로 공간에서 수평 또는 수직으로 한 칸씩 이동할 때, 지정된 위치에서 이동가능한 위치를 찾아 이동할 수 있는 빈 공간을 좌표를 MazeLocation으로 구성된 List로 반환한다.
2.2.3 깊이 우선 탐색
깊이 우선 탐색(Depth-First-Search)은 막다른 지점에 도달하여 최종 결정 지점으로 되돌아오기 전까지 가능한 깊이 탐색한다.
DFS 알고리즘은 스택(Last In First out) 자료구조에 의존한다.
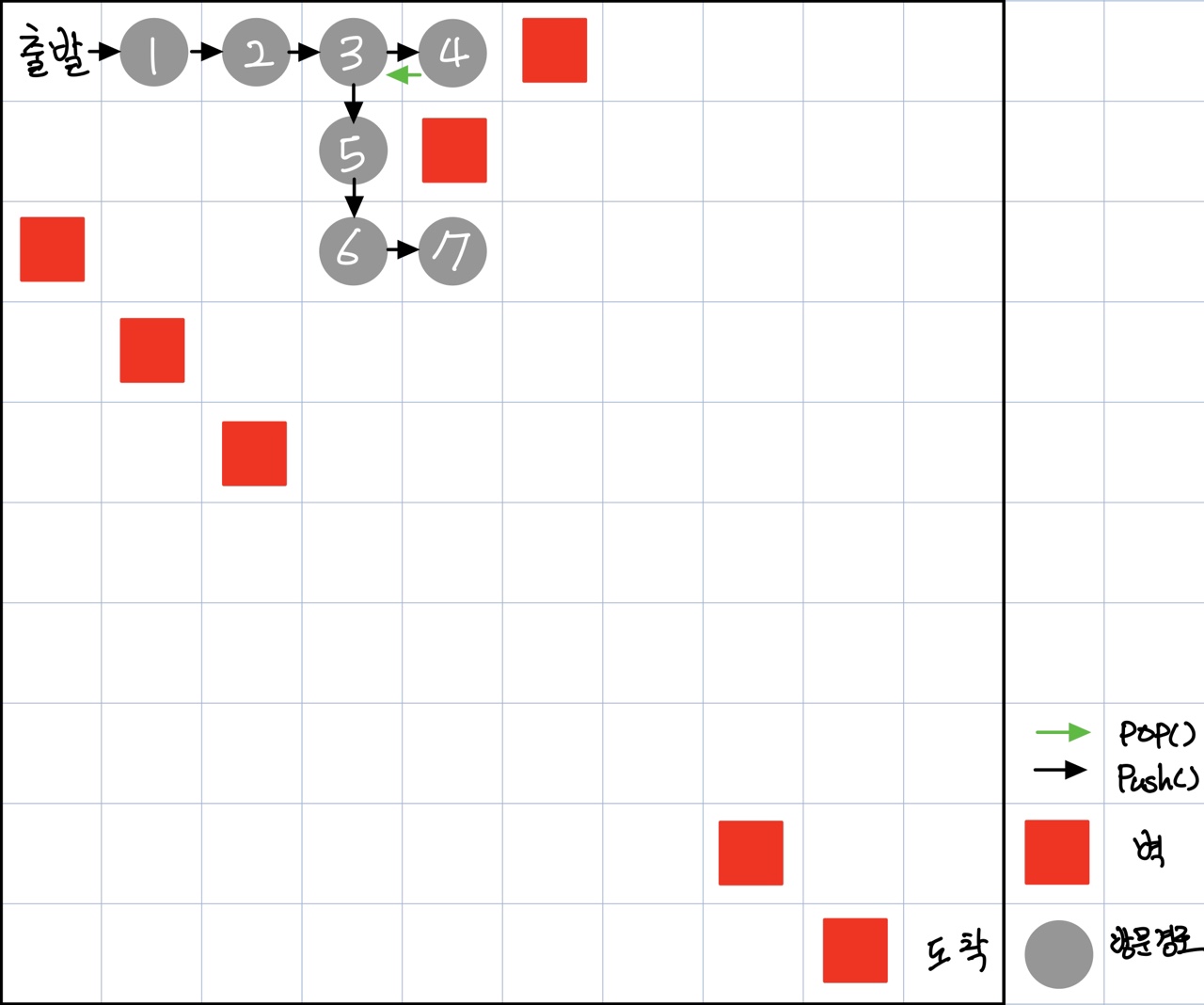
push() 와 pop() 메서드와 스택이 비었는지 확인하는 메소드를 포함한 스택 코드를 generic_search.py에 추가한다.
# generic_search.py
...
class Stack(Generic[T]):
def __init__(self) -> None:
self._container: List[T] = []
@property
def empty(self) -> bool:
return not self._container # 스택이 비었다면 true(= false 가 아니다)
def push(self, item: T) -> None:
self._container.append(item)
def pop(self) -> T:
return self._container.pop() # 후입선출(LIFO)
def __repr__(self) -> str:
return repr(self._container)
탐색은 한 장소에서 다른 장소의 변화를 추적하기 위해 Node 클래스가 필요하다.
미로 찾기에서 노드는 장소를 감싼 wrapper로 생각할 수 있다. 노드는 부모 노드에서 온 한 장소를 의미한다.
Node 클래스는 cost 와 heuristic 속성이 있고 __lt__() 특수 메서드를 구현하여 정의한다.
#generic_search.py
...
class Node(Generic[T]):
def __init__(self, state: T, parent: Optional[Node], cost: float = 0.0,
heuristic: float = 0.0) -> None:
self.state: T = state
self.parent: Optional[Node] = parent
self.cost: float = cost
self.heuristic: float = heuristic
def __lt__(self, other: Node) -> bool:
return (self.cost + self.heuristic) < (other.cost + other.heuristic)
NOTE: Optional 매개변수는 매개변수가 있다면 해당 타입의 값이 참조되거나 None 이 참조될 수 있음을 의미한다.
NOTE: generic_search.py 파일 맨위 from __future__ import annotations 문은 노드가 자신의 메서드 힌트 타입을 참조하도록 허용한다. 이를 사용하지 않는다면 타입힌트를 ‘Node’와 같이 따옴표를 사용해야한다.
깊이 우선탐색 과정
- 탐색 방문하려고 하는 장소
Stack으로 다음 코드에서frontier변수로 표현한다. - 이미 방문한 장소를
Set자료형인explored변수로 표현한다. frontier변수의pop()한 곳이 목표 지점인지 확인한다.(목표 지점에 도달할 시 종료)successors변수의 현재지점에서 다음 이동할 수 있는 장소를frontier변수에push()한다.frontier변수가 비어 있다면 모든 장소를 방문했으므로 탐색 종료한다.
#generic_search.py
...
def dfs(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]]) -> Optional[Node[T]]:
# frontier 방문하지 않은 곳
frontier: Stack[Node[T]] = Stack()
frontier.push(Node(initial, None))
# explored 이미 방문 한 곳
explored: Set[T] = {initial}
# 방문할 곳이 있는지 탐색
while not frontier.empty:
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표지점에 도달시 탐색종료
if goal_test(current_state):
return current_node
# 방문하지 않은 장소가 있는지 확인
for child in successors(current_state):
if child in explored: #이미 방문한 자식 노드(장소)일시 건너뜀
continue
explored.add(child)
frontier.push(Node(child, current_node))
return None # 탐색 결과 목표지점에 도달하지 못함
dfs() 함수에서 목표 지점을 찾았다면 목표 지점 경로를 캡슐화한 노드(Node)를 반환한다.
출발지점에서부터 목표지점까지 경로는 노드의 parent 속성을 사용하여 reverse 함으로써 재구성할 수 있다.
#generic_search.py
..
def node_to_path(node: Node[T]) -> List[T]:
path: List[T] = [node.state]
# reverse
while node.parent is not None:
node = node.parent
path.append(node.state)
path.reverse()
return path
미로의 출발 지점, 목표 지점, 경로를 출력하기 위해 maze.py의 Maze 클래스에 두 메서드를 추가한다.
# class Maze 계속
...
def mark(self, path: List[MazeLocation]):
for maze_location in path:
self._grid[maze_location.row][maze_location.column] = Cell.PATH
self._grid[self.start.row][self.start.column] = Cell.START
self._grid[self.goal.row][self.goal.column] = Cell.GOAL
def clear(self, path: List[MazeLocation]):
for maze_location in path:
self._grid[maze_location.row][maze_location.column] = Cell.EMPTY
self._grid[self.start.row][self.start.column] = Cell.START
self._grid[self.goal.row][self.goal.column] = Cell.GOAL
# dfs 실행결과
m: Maze = Maze()
print(m)
print("=" * 12)
solution1: Optional[Node[MazeLocation]] = dfs(m.start, m.goal_test, m.successors)
if solution1 is None:
print("깊이 우선 탐색으로 길을 찾을 수 없습니다.")
else:
path1: List[MazeLocation] = node_to_path(solution1)
m.mark(path1)
print(m)
m.clear(path1)
S X X
X
X X
X
X X
X XXX
X
XX X
XXX G
============
S*X X
*******
*X
X**** X
X****
* X X
X******XXX
X ***
XX *X
XXX *G
2.2.4 너비 우선 탐색
깊이 우선 탐색으로 찾은 목표 지점에 대한 경로는 부자연스럽게 보일 수 있으며, 최단 경로가 아닐 수 있다.
너비 우선 탐색(Breadth-First-Search)은 탐색의 각 반복마다 출발 지점에서 같은 깊이의 노드를 가까운 지점부터 순차적으로 탐색함으로써 항상 최단 경로를 찾는다.
깊이 우선 탐색은 일반적으로 너비 우선 탐색보다 빨리 목표 지점을 찾을 가능성이 크다. 따라서 최단 경로를 선택하느냐 빠른 탐색의 가능성을 선택하느냐에 탐색 방법을 달리 할 수 있다.
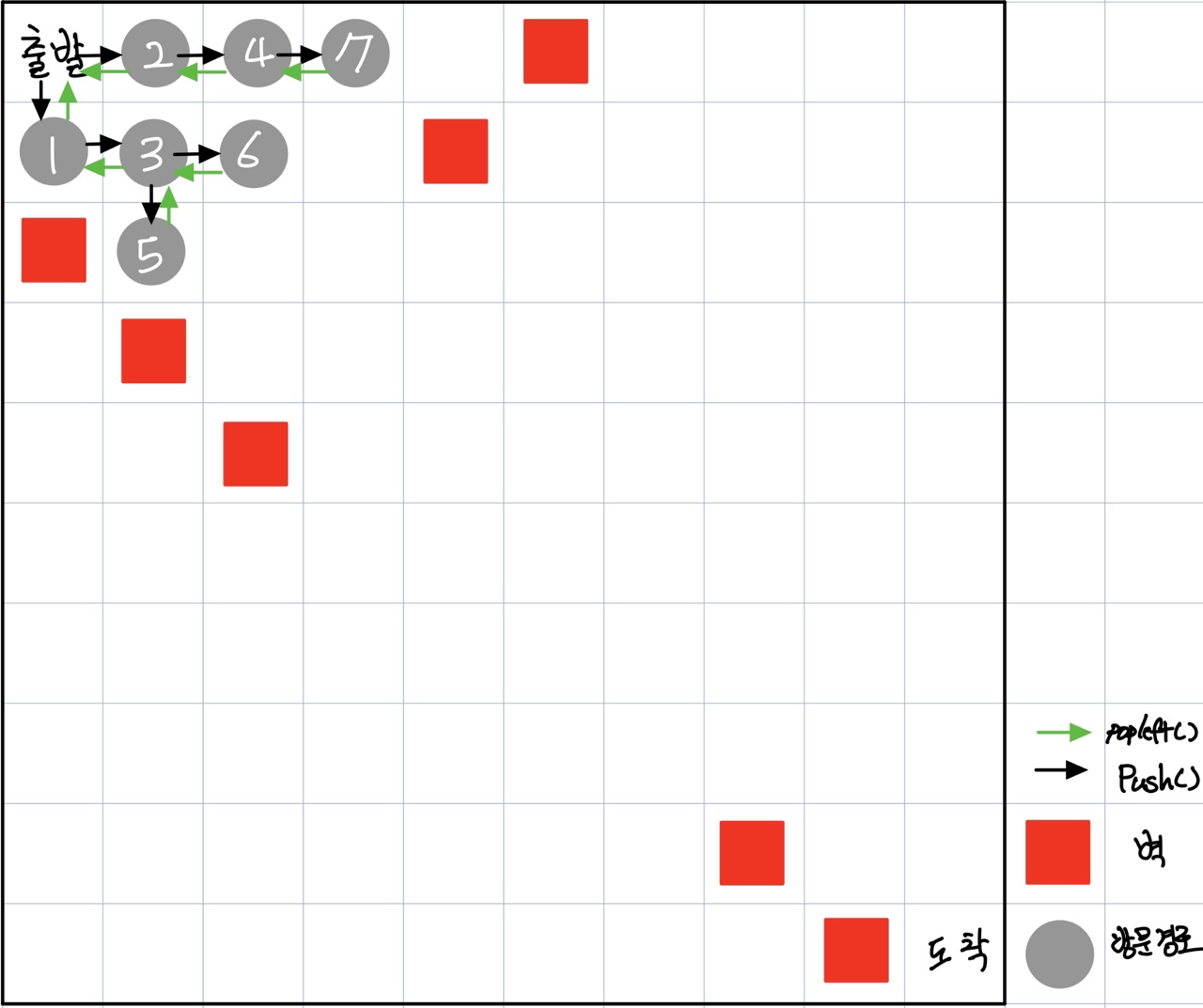
큐 자료구조
너비 우선 탐색을 구현하려면 큐 자료구조가 필요하다. 스택과 다르게 선입선출(First-In-First-Out)인 자료구조이다.
큐에는 스택과 같이 push() 와 pop() 메서드가 있다. 다른 점은 _container 변수에서 오른쪽 끝 요소 대신 왼쪽 끝 요소를 제거하고 반환한다. 또한 리스트 대신 덱(deque)을 사용한다.
#generic_search 계속
...
class Queue(Generic[T]):
def __init__(self) -> None:
self._container: Deque[T] = Deque()
@property
def empty(self) -> bool:
return not self._container # 요소가 없을시에 true 반환 (= false가 아니다)
def push(self, item: T) -> None:
self._container.append(item)
def pop(self) -> T:
return self._container.popleft() # 가장 왼쪽에 있는 요소 제거 및 반환
def __repr__(self) -> str:
return repr(self._container)
NOTE: 큐 구현을 Deque을 사용하는 이유는 pop() 메서드를 통해 왼쪽에 있는 요소를 제거해야되는데 List에서 왼쪽 요소를 제거하는 것은 비효율적이다. 하지만 덱은 양쪽에서 효율적으로 popleft() 메서드를 통해 효율적으로 처리 가능하다.
| 메서드 | 시간복잡도 |
|---|---|
| (덱) popleft() | O(1) |
| (리스트) pop(0) | O(n) |
너비 우선 탐색은 깊이 우선 탐색 알고리즘과 동일하며, frontier 변수 타입만 스택에서 큐로 변경되었다.
타입 변경으로 탐색 순서가 변경되고, 출발 지점에서 가장 가까운 지점을 먼저 탐색한다.
#generic_search.py 계속
def bfs(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]]) -> Optional[Node[T]]:
# frontier 아직 방문하지 않은 곳
frontier: Queue[Node[T]] = Queue()
frontier.push(Node(initial, None))
# explored 이미 방문한 곳
explored: Set[T] = {initial}
# 방문할 곳이 있는지 탐색
while not frontier.empty:
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표 지점에 도달하면 탐색 종료
if goal_test(current_state):
return current_node
# 방문하지 않은 장소가 있는지 확인
for child in successors(current_state):
if child in explored: # 이미 방문한 노드 건더뜀
continue
explored.add(child)
frontier.push(Node(child, current_node))
return None # 탐색 결과 목표지점에 도달하지 못함
print("너비 우선 탐색")
solution2: Optional[Node[MazeLocation]] = bfs(m.start, m.goal_test, m.successors)
if solution2 is None:
print("너비 우선 탐색으로 길을 찾을 수 없습니다.")
else:
path2: List[MazeLocation] = node_to_path(solution2)
m.mark(path2)
print(m)
m.clear(path2)
print("="*12)
print("깊이 우선 탐색")
solution1: Optional[Node[MazeLocation]] = dfs(m.start, m.goal_test, m.successors)
if solution1 is None:
print("깊이 우선 탐색으로 길을 찾을 수 없습니다.")
else:
path1: List[MazeLocation] = node_to_path(solution1)
m.mark(path1)
print(m)
m.clear(path1)
너비 우선 탐색
S X X
*
* X
** X X
X*
* X X
X***** XXX
X*
XX * X
XXX****G
============
깊이 우선 탐색
S*X X
*******
*X
X**** X
X****
* X X
X******XXX
X ***
XX *X
XXX *G
2.2.5 $A^*$ 알고리즘
너비 우선 탐색은 모든 경우를 다루기 때문에 시간이 많이 걸릴 수 있다.
너비 우선 탐색과 마찬가지로 $A^*$알고리즘은 출발 지점에서 목표 지점까지 최단 경로를 찾는 것을 목표로 한다.
$A^*$알고리즘은 cost 함수와 heuristic 함수를 사용하기 때문에 목표 지점에 가장 빨리 도달할 가능성이 있는 경로 탐색에 집중한다.
- 비용 함수
g(n)은 특정 지점에 도달하기 위한 비용을 구한다. - 휴리스틱함수
h(n)은 해당 지점에서 목표 지점까지의 비용을 추정한다. h(n)이 허용 가능한 휴리스틱이라면 최적의 경로로 판단한다.
탐색을 고려하는 모든 지점에 대한 총 비용을
f(n)이라고 할 때,f(n) = g(n) + h(n)이다. $A^*$ 알고리즘은f(n)이 최소화 되는 경로를 선택한다.
우선순위 큐 자료구조
최소의 f(n) 을 구하기 위해 $A^*$ 알고리즘은 우선순위 큐 자료구조를 사용한다.
우선순위 큐의 요소는 내부 순서를 유지하며, 첫 번째 가장 우선순위가 높은 요소이다.
f(n)이 낮은 노드가 우선순위가 높다.
우선순위 큐는 보통 이진 힙을 내부적으로 사용하며, push()와 pop()의 시간복잡도는 $O(log_2 n)$ 이다.
PriorityQueue 클래스는 Stack , Queue 클래스의 push() , pop() 메서드에서 각각 heappush() , heappop() 함수를 사용하도록 수정한다.
#generic_search 계속
class PriorityQueue(Generic[T]):
def __init__(self) -> None:
self._container: List[T] = []
@property
def empty(self) -> bool:
return not self._container # 요소가 없을시에 true 반환 (= false가 아니다)
def push(self, item: T) -> None:
heappush(self._container, item) # 우선순위 push()
def pop(self) -> T:
return heappop(self._container) # 우선순위 pop()
def __repr__(self) -> str:
return repr(self._container)
경로의 우선순위를 결정하기 위해 heappush() 와 heappop() 함수에 < 연산자를 사용하여 비교한다.
위에 generic_search.py의 Node 클래스에서 __lt__() 특수 메서드를 사용한다.
휴리스틱
휴리스틱은 문제 해결방법을 직관적으로 제시한다.
미로 찾기의 경우, 방문하지 않은 지점 중 어느 노드가 가장 목표 지점에 가까운지 찾는다.
허용 가능한 휴리스틱(목표 도달 추정 비용 < 경로에서 현재 지점의 최저 가능 비용)안에 경로에 최단 경로가 포함되어있다. 이상적인 휴리스틱은 지점을 모두 탐색하지 않고 가능한 실제 최단 경로에 가까운 경로를 찾는 것이다.
속도와 정확성의 tradeoff 속에서 적절한 휴리스틱 함수를 구성하는 것이 중요하다.
유클리드 거리
두 점 사이의 최단 거리는 직선이다. 미로 찾기 문제의 휴리스틱에서는 유클리드 거리를 통해 휴리스틱을 계산한다.
피타고라스 정리에서 파생된 유클리드 거리는 $\sqrt{(두 x 좌표의 차이)^2 + (두 y 좌표의 차이)^2}$
두 x 좌표의 차이는 미로에서 열의 차와 같다. 두 y 좌표의 차이는 미로에서 행의 차이와 같다.
#maze.py 계속
def euclidean_distance(goal: MazeLocation) -> Callable[[MazeLocation, float]]:
def distance(ml: MazeLocation) -> float:
xdist: int = ml.column - goal.column
ydist: int = ml.row - goal.row
return sqrt((xdist * xdist) + (ydist * ydist))
return distance
NOTE: 위 eulidean_distance() 함수는 distance() 함수를 반환한다. 파이썬은 일급 함수(First-class function)을 지원함으로 이와 같은 패턴을 사용할 수 있다. distance() 함수는 euclidean_distance() 함수에서 전달받은 MazeLocation 네임드튜플의 goal 변수를 캡쳐링한다.
캡쳐링은 distance()함수가 호출될 때마다 영구적으로 goal 변수를 참조하여 목표 지점까지 거리를 계산한다. 이 패턴을 사용하면 더 적은 수의 매개변수를 필요로 하는 함수를 만들 수 있다.
맨해튼 거리
격자 모양의 뉴욕의 맨해튼 거리를 탐색하는 것에서 유래되었다. 네 방향 중 한 방향으로만 움직일 수 있는 미로의 예시에서 효율적일 수 있다.
#maze.py 계속
def manhattan_distance(goal: MazeLocation) -> Callable[[MazeLocation], float]:
def distance(ml: MazeLocation) -> float:
xdist: int = abs(ml.column - goal.column)
ydist: int = abs(ml.row - goal.row)
return (xdist + ydist)
return distance
$A^*$ 알고리즘 구현
frontier변수 타입을 큐에서 우선순위 큐로 변경한다.frontier변수는 우선순위가 가장 높은(f(n)이 최소인) 노드를pop()한다.explored변수의 타입을Set에서Dict로 변경한다. 방문할 수 있는 각 노드의 최저 비용(g(n))을 축적할 수 있다.- 휴리스틱 함수를 사용했을 때, 노드의 휴리스틱 값이 일치하지 않으면 일부 노드는 두번 방문될 수 있다.
- 새로운 방향에서 발견된 노드가 방문했던 노드보다 비용이 적으면 새 방향의 경로를 더 선호한다.
astar() 함수는 비용 함수를 사용하지 않는다. 대신 모든 미로의 거리 비용을 1로 간주한다. 각 노드는 heuristic() 함수를 사용하여 비용이 할당된다.
#generic_search 계속
def astar(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]],
heuristic: Callable[[T], float]) -> Optional[Node[T]]:
# frontier 아직 방문하지 않은 곳
frontier: PriorityQueue[Node[T]] = PriorityQueue()
frontier.push(Node(initial, None, 0.0, heuristic(initial)))
# explored 이미 방문한 곳
explored: Dict[T, float] = {initial: 0.0}
# 방문할 곳이 더 있는지 탐색
while not frontier.empty:
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표 지점에 도달하면 탐색 종료
if goal_test(current_state):
return current_node
# 방문하지 않은 다음 장소가 있는지 확인
for child in successors(current_state):
new_cost: float = current_node.cost + 1 # 다음 노드까지의 비용은 1
if child not in explored or explored[child] > new_cost:
explored[child] = new_cost
frontier.push(Node(child, current_node, new_cost, heuristic(child)))
return None # 탐색 결과 목표지점에 도달하지 못함
print("<너비 우선 탐색>")
solution2: Optional[Node[MazeLocation]] = bfs(m.start, m.goal_test, m.successors)
if solution2 is None:
print("너비 우선 탐색으로 길을 찾을 수 없습니다.")
else:
path2: List[MazeLocation] = node_to_path(solution2)
m.mark(path2)
print(m)
m.clear(path2)
print("="*12)
print("<A* 알고리즘>")
distance: Callable[[MazeLocation], float] = manhattan_distance(m.goal)
solution3: Optional[Node[MazeLocation]] = astar(m.start, m.goal_test, m.successors, distance)
if solution3 is None:
print("A* 알고리즘으로 길을 찾을 수 없습니다.")
else:
path3: List[MazeLocation] = node_to_path(solution3)
m.mark(path3)
print(m)
<너비 우선 탐색>
S X X
*
* X
** X X
X*
* X X
X***** XXX
X*
XX * X
XXX****G
============
<A* 알고리즘>
S X X
*
* X
** X X
X******
X*X
X *XXX
X ***
XX *X
XXX *G
깊이 우선 탐색과 너비 우선 탐색은 성능이 중요하지 않은 소규모 데이터셋과 공간에 적합하다.
bfs()와 astar() 함수가 모두 최적의 경로를 찾고 있음에도 출력 결과는 서로 다를 수 있다. astar() 함수는 휴리스틱 때문에 대각선으로 목표 지점을 향한다.
적절한 휴리스틱 함수를 적용한 $A^*$ 알고리즘은 최적의 경로를 제공할 뿐아니라 너비 우선 탐색보다 성능이 훨씬 좋다.
astar()함수는bfs()함수보다 더 적은 수의 노드를 검색하므로 성능이 더 좋다.
2.3 선교사와 식인종 문제
- 세명의 선교사와 세명의 식인종이 강 서쪽에 있다.
- 두명이 탈 수 있는 배를 가지고 있으며, 배를 타고 동쪽으로 이동해야한다.
- 강 양쪽에 선교사보다 더 많은 식인종이 있다면 식인종은 선교사를 잡아먹는다.
- 강을 건널 때 배에는 적어도 한 명이 탑승해야 한다.
2.3.1 문제
서쪽 강둑에 선교사와 식인종이 몇명 있는가?와 배가 서쪽에 있는가? 이 두 질문을 파악할 수 있으면 전체에 어떻게 퍼져 있는지 확인 할 수 있다.
# missionaries.py
from __future__ import annotations
from typing import List, Optional
from generic_search import bfs, Node, node_to_path
MAX_NUM : int = 3
class MCState:
def __init__(self, missionaries: int, cannibals: int, boat: bool) -> None:
self.wm: int = missionaries # 서쪽 강둑에 있는 선교사의 수
self.wc: int = cannibals # 서쪽 강둑에 있는 식인종의 수
self.em: int = MAX_NUM - self.wm # 동쪽 강둑에 있는 선교사의 수
self.ec: int = MAX_NUM - self.wc # 동쪽 강둑에 있는 식인종의 수
self.boat: bool = boat
def __str__(self) -> str:
return (f"서쪽 강둑에는 {self.wm}명의 선교사와 {self.wc}명의 식인종이 있다. \n"+
f"동쪽 강둑에는 {self.em}명의 선교사와 {self.ec}명의 식인종이 있다. \n"+
f"배는 {'서' if self.boat else '동'}쪽에 있다.")
def goal_test(self) -> bool:
return self.is_legal and self.em == MAX_NUM and self.ec == MAX_NUM
@property
def is_legal(self) -> bool:
if self.wm < self.wc and self.wm > 0:
return False
if self.em < self.ec and self.em > 0:
return False
return True
def successors(self) -> List[MCState]:
sucs: List[MCState] = []
if self.boat: # 서쪽에 배 존재
if self.wm > 1:
sucs.append(MCState(self.wm - 2, self.wc, not self.boat))
if self.wm > 0:
sucs.append(MCState(self.wm - 1, self.wc, not self.boat))
if self.wc > 1:
sucs.append(MCState(self.wm, self.wc - 2, not self.boat))
if self.wc > 0:
sucs.append(MCState(self.wm, self.wc - 1, not self.boat))
if (self.wc > 0) and (self.wm > 0):
sucs.append(MCState(self.wm - 1, self.wc - 1, not self.boat))
else: # 동쪽에 배 존재
if self.em > 1:
sucs.append(MCState(self.wm + 2, self.wc, not self.boat))
if self.em > 0:
sucs.append(MCState(self.wm + 1, self.wc, not self.boat))
if self.ec > 1:
sucs.append(MCState(self.wm, self.wc + 2, not self.boat))
if self.ec > 0:
sucs.append(MCState(self.wm, self.wc + 1, not self.boat))
if (self.ec > 0) and (self.em >0):
sucs.append(MCState(self.wm + 1, self.wc + 1, not self.boat))
return [x for x in sucs if x.is_legal]
goal_test() 는 동쪽 강둑으로 선교사 3명과 식인종 3명이 이동했을 경우, 목표 상태 확인을 위한 함수이다.
is_legal() 이동하는 과정에서 합법적인 상태(선교사 >= 식인종)규칙을 판단하기 위한 함수이다.
successors() 함수는 한 강둑에서 다른 강둑으로 이동 가능한 모든 상태를 확인한 다음 합법적인 상태인지 검사하고 이동할 수 있는 경우의 수를 List로 반환한다.
2.3.2 문제풀이
bfs() , dfs() , astar() 함수로 선교사와 식인종 문제를 풀기 전 솔루션으로 이어지는 상태리스트를 이해하기 쉽게 출력하는 함수가 필요하다.
#missionaries.py 계속
def display_solution(path: List[MCState]):
if len(path) == 0: # 세니티 체크
return
old_state: MCState = path[0]
print(old_state)
for current_state in path[1:]:
if current_state.boat:
print(f"{old_state.em - current_state.em}명의 선교사와
{old_state.ec - current_state.ec}명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.\n")
else:
print(f"{old_state.wm - current_state.wm}명의 선교사와
{old_state.wc - current_state.wc}명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.\n")
print(current_state)
old_state = current_state
start: MCState = MCState(MAX_NUM, MAX_NUM, True)
solution: Optional[Node[MCState]] = bfs(start, MCState.goal_test, MCState.successors)
if solution is None:
print("답을 찾을 수 없습니다.")
else:
path: List[MCState] = node_to_path(solution)
display_solution(path)
서쪽 강둑에는 3명의 선교사와 3명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 0명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 2명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 3명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 2명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 3명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 1명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 2명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 3명의 선교사와 0명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 3명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 2명의 식인종이 있다.
배는 서쪽에 있다.
2명의 선교사와 0명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 1명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 2명의 선교사와 2명의 식인종이 있다.
배는 동쪽에 있다.
1명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 2명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 1명의 선교사와 1명의 식인종이 있다.
배는 서쪽에 있다.
2명의 선교사와 0명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 3명의 선교사와 1명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
동쪽 강둑에는 3명의 선교사와 0명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 2명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 3명의 선교사와 2명의 식인종이 있다.
배는 동쪽에 있다.
1명의 선교사와 0명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 1명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 2명의 선교사와 2명의 식인종이 있다.
배는 서쪽에 있다.
1명의 선교사와 1명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 0명의 식인종이 있다.
동쪽 강둑에는 3명의 선교사와 3명의 식인종이 있다.
배는 동쪽에 있다.
연습문제
1번
dna_search.py에서 숫자가 100만 개인 정렬된 리스트를 생성하고 선형 검색의 linear_contains() 와 이진 검색 binary_contains() 함수를 사용하여 몇몇 숫자를 찾는데 걸리는 시간을 측정하라.
from typing import TypeVar, Iterable, Generic, Sequence, List, Optional, Any
from typing_extensions import Protocol
T = TypeVar('T')
def make_list() -> List[T]:
sorted_list: List[T] = [x for x in range(1, 1000000)]
return sorted_list
def linear_contains(iterable: Iterable[T], key: T) -> bool:
for item in iterable:
if item == key:
return True
return False
C = TypeVar('C', bound = "Comparable")
class Comparable(Protocol):
def __eq__(self, other: Any) -> bool:
return self == other
def __lt__(self: C, other: C) -> bool:
return not (self > other) and self != other
def __gt__(self: C, other: C) -> bool:
return (not self < other) and self != other
def __le__(self: C, other: C) -> bool:
return self < other or self == other
def __ge__(self: C, other: C) -> bool:
return not self < other
def binary_contains(sequence: Sequence[C], key: C) -> bool:
low: int = 0
high: int = len(sequence) - 1
while low <= high: # 검색 공간이 존재
mid: int = (low + high) // 2
if sequence[mid] < key:
low = mid + 1
elif sequence[mid] > key:
high = mid - 1
else:
return True
return False
import time
sorted_time = make_list()
search_list = [1, 5000, 500000, 1000000, 1000001]
for search in search_list:
linear_st = time.time()
linear_bool = linear_contains(sorted_time, search)
linear_et = time.time()
binary_st = time.time()
binary_bool = binary_contains(sorted_time, search)
binary_et = time.time()
print(f"{search} 검색에 대한 시간 \n"+
f"linear search = {linear_et - linear_st:10.9f} 초\n"+
f"binary search = {binary_et - binary_st:10.9f} 초\n")
1 검색에 대한 시간
linear search = 0.000000000 초
binary search = 0.000000000 초
5000 검색에 대한 시간
linear search = 0.000998497 초
binary search = 0.000000000 초
500000 검색에 대한 시간
linear search = 0.022004366 초
binary search = 0.000000000 초
1000000 검색에 대한 시간
linear search = 0.033698559 초
binary search = 0.000000000 초
1000001 검색에 대한 시간
linear search = 0.065702200 초
binary search = 0.000000000 초
- 정렬된 리스트에 요소가 있을 경우
linear search는 매우 앞쪽에 정렬된 데이터를 찾는 경우에 관해서 빠른 속도를 보이지만 뒤쪽에 정렬된 요소를 찾는 경우는 느린 속도를 보인다.binary search는 앞쪽에 정렬된 데이터와 뒤쪽에 정렬된 데이터의 차이가 거의 없이 빠른 속도를 보인다.
- 정렬된 리스트에 없는 요소를 찾는 경우
linear search는 가장 오랜 시간이 걸린다.binary search는 일관적으로 빠른 속도를 보인다.
| 최선 | 평균 | 최악 | |
|---|---|---|---|
| linear search | $O(1)$ | $O(\frac{n}{2})$ | $O(n)$ |
| binary search | $O(\log_2 n)$ | $O(\log_2 n)$ | $O(\log_2 n)$ |
2번
dfs(), bfs(), astar() 함수에 카운터를 추가하여 동일한 미로를 검색하는 지점의 수를 확인하라. 통계적으로 의미 있는 결과를 얻기 위해 100개의 미로 샘플에 대해 조사한다.
from __future__ import annotations
from typing import TypeVar, Iterable, Sequence, Generic, List, Callable, Set, Deque, Dict, Any, Optional
from typing_extensions import Protocol
from heapq import heappush, heappop
T = TypeVar('T')
...
def dfs(initial: T, goal_test: Callable[[T], bool],
successors: Callable[[T], List[T]]) -> int:
count = 0
# frontier 방문하지 않은 곳
frontier: Stack[Node[T]] = Stack()
frontier.push(Node(initial, None))
# explored 이미 방문 한 곳
explored: Set[T] = {initial}
# 방문할 곳이 있는지 탐색
while not frontier.empty:
count += 1
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표지점에 도달시 탐색종료
if goal_test(current_state):
return count
# 방문하지 않은 장소가 있는지 확인
for child in successors(current_state):
if child in explored: #이미 방문한 자식 노드(장소)일시 건너뜀
continue
explored.add(child)
frontier.push(Node(child, current_node))
return 67 # 탐색 결과 목표지점에 도달하지 못함
def bfs(initial: T, goal_test: Callable[[T], bool],
successors: Callable[[T], List[T]]) -> int:
count = 0
# frontier 아직 방문하지 않은 곳
frontier: Queue[Node[T]] = Queue()
frontier.push(Node(initial, None))
# explored 이미 방문한 곳
explored: Set[T] = {initial}
# 방문할 곳이 있는지 탐색
while not frontier.empty:
count += 1
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표 지점에 도달하면 탐색 종료
if goal_test(current_state):
return count
# 방문하지 않은 장소가 있는지 확인
for child in successors(current_state):
if child in explored: # 이미 방문한 노드 건더뜀
continue
explored.add(child)
frontier.push(Node(child, current_node))
return 76 # 탐색 결과 목표지점에 도달하지 못함
def astar(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]],
heuristic: Callable[[T], float]) -> int:
count = 0
# frontier 아직 방문하지 않은 곳
frontier: PriorityQueue[Node[T]] = PriorityQueue()
frontier.push(Node(initial, None, 0.0, heuristic(initial)))
# explored 이미 방문한 곳
explored: Dict[T, float] = {initial: 0.0}
# 방문할 곳이 더 있는지 탐색
while not frontier.empty:
count += 1
current_node: Node[T] = frontier.pop()
current_state: T = current_node.state
# 목표 지점에 도달하면 탐색 종료
if goal_test(current_state):
return count
# 방문하지 않은 다음 장소가 있는지 확인
for child in successors(current_state):
new_cost: float = current_node.cost + 1 # 다음 노드까지의 비용은 1
if child not in explored or explored[child] > new_cost:
explored[child] = new_cost
frontier.push(Node(child, current_node, new_cost, heuristic(child)))
return 85 # 탐색 결과 목표지점에 도달하지 못함
import numpy as np
count_list = np.empty((0,3), int)
for _ in range(100):
maze: Maze = Maze()
count_by_search: List[int, int, int] = [dfs(maze.start, maze.goal_test, maze.successors),
bfs(maze.start, maze.goal_test, maze.successors),
astar(maze.start, maze.goal_test, maze.successors, manhattan_distance(maze.goal))]
count_list = np.append(count_list, np.array([count_by_search]), axis = 0)
count_mean = count_list.mean(axis=0)
print(f"dfs 알고리즘의 평균 방문 노드의 수 {count_mean[0]}\n",
f"bfs 알고리즘의 평균 방문 노드의 수 {count_mean[1]}\n",
f"astar 알고리즘의 평균 방문 노드의 수 {count_mean[2]}")
dfs 알고리즘의 평균 방문 노드의 수 58.88
bfs 알고리즘의 평균 방문 노드의 수 81.35
astar 알고리즘의 평균 방문 노드의 수 59.54
dfs() , bfs() , astar() 알고리즘에 경로를 탐색하는 가지의 수를 count 변수로 세어 반환한다.
maze가 랜덤하게 100번 생성되는 count 개수를 2차원 numpy array로 만든 후 numpy 모듈의 mean() 평균값을 구하는 메서드를 활용하여 평균값을 구한다.
경로를 찾지 못하는 경우 None을 반환하게 되면 평균을 구하지 못함으로 평균 방문 노드의 수의 예상치를 반환시켰다.
- dfs()의 경우, 방문하는 노드의 최단거리는 18회 최장거리는 99회 이므로 $\frac{18+99}{2} \approx$ 67을 반환한다.
- bfs()의 경우, 목표 노드에 인접한 노드까지 경우가 95개 중 장애물의 임곗값이 20% 이므로 $95 * 0.2$ = 76을 반환한다.
- astar()의 경우, 4방향으로 움직일 수 있는 노드에서 최적의 경로를 찾는 예상치 58를 반환한다.
평균 방문노드의 수는 dfs가 가장 적지만 최적의 경로를 알려주지 못하는 단점을 가진다.
최적의 경로를 찾는 알고리즘 중 astar 알고리즘이 평균 방문 노드의 수가 적기 때문에 더 효율적이라고 할 수 있다.
3번
선교사와 식인종 수를 변형하여 문제를 풀어보라(힌트 : MCState 클래스에 __eq__() 및 __hash()__ 특수 메서드를 구현한다.
# missionaries.py 수정
MAX_NUM : int = 5
# MCState class 수정
...
def __eq__(self, other) -> bool:
return self.wm == other.wm and self.wc == other.wc and self.boat == other.boat
def __hash__(self):
return hash((self.wm, self.wc, self.boat))
def successors(self) -> List[MCState]:
sucs: List[MCState] = []
if self.boat: # 서쪽에 배 존재
if self.wm > 2:
sucs.append(MCState(self.wm - 3, self.wc, not self.boat))
if self.wm > 1:
sucs.append(MCState(self.wm - 2, self.wc, not self.boat))
if self.wm > 0:
sucs.append(MCState(self.wm - 1, self.wc, not self.boat))
if self.wc > 2:
sucs.append(MCState(self.wm, self.wc - 3, not self.boat))
if self.wc > 1:
sucs.append(MCState(self.wm, self.wc - 2, not self.boat))
if self.wc > 0:
sucs.append(MCState(self.wm, self.wc - 1, not self.boat))
if (self.wc > 1) and (self.wm > 0):
sucs.append(MCState(self.wm - 1, self.wc - 2, not self.boat))
if (self.wc > 0) and (self.wm > 1):
sucs.append(MCState(self.wm - 2, self.wc - 1, not self.boat))
if (self.wc > 0) and (self.wm > 0):
sucs.append(MCState(self.wm - 1, self.wc - 1, not self.boat))
else: # 동쪽에 배 존재
if self.em > 2:
sucs.append(MCState(self.wm + 3, self.wc, not self.boat))
if self.em > 1:
sucs.append(MCState(self.wm + 2, self.wc, not self.boat))
if self.em > 0:
sucs.append(MCState(self.wm + 1, self.wc, not self.boat))
if self.ec > 2:
sucs.append(MCState(self.wm, self.wc + 3, not self.boat))
if self.ec > 1:
sucs.append(MCState(self.wm, self.wc + 2, not self.boat))
if self.ec > 0:
sucs.append(MCState(self.wm, self.wc + 1, not self.boat))
if (self.ec > 1) and (self.em > 0):
sucs.append(MCState(self.wm + 1, self.wc + 2, not self.boat))
if (self.ec > 0) and (self.em > 1):
sucs.append(MCState(self.wm + 2, self.wc + 1, not self.boat))
if (self.ec > 0) and (self.em > 0):
sucs.append(MCState(self.wm + 1, self.wc + 1, not self.boat))
return [x for x in sucs if x.is_legal]
...
-
MAX_NUM = 5선교사와 식인종은 각각 5명으로 증가 -
successors()보트를 3명 탈 수 있을 때, 이동 가능한 경우 추가
start: MCState = MCState(MAX_NUM, MAX_NUM, True)
solution: Optional[Node[MCState]] = bfs(start, MCState.goal_test, MCState.successors)
if solution is None:
print("답을 찾을 수 없습니다.")
else:
path: List[MCState] = node_to_path(solution)
display_solution(path)
서쪽 강둑에는 5명의 선교사와 5명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 0명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 3명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 5명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 2명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 5명의 선교사와 4명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 1명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 3명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 5명의 선교사와 1명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 4명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 5명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
배는 서쪽에 있다.
3명의 선교사와 0명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 2명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 3명의 선교사와 3명의 식인종이 있다.
배는 동쪽에 있다.
1명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 3명의 선교사와 3명의 식인종이 있다.
동쪽 강둑에는 2명의 선교사와 2명의 식인종이 있다.
배는 서쪽에 있다.
3명의 선교사와 0명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
동쪽 강둑에는 5명의 선교사와 2명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 2명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 5명의 식인종이 있다.
동쪽 강둑에는 5명의 선교사와 0명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 3명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 2명의 식인종이 있다.
동쪽 강둑에는 5명의 선교사와 3명의 식인종이 있다.
배는 동쪽에 있다.
0명의 선교사와 1명의 식인종이 동쪽 강둑에서 서쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 3명의 식인종이 있다.
동쪽 강둑에는 5명의 선교사와 2명의 식인종이 있다.
배는 서쪽에 있다.
0명의 선교사와 3명의 식인종이 서쪽 강둑에서 동쪽 강둑으로 갔다.
서쪽 강둑에는 0명의 선교사와 0명의 식인종이 있다.
동쪽 강둑에는 5명의 선교사와 5명의 식인종이 있다.
배는 동쪽에 있다.
NOTE: __hash__() 와 __eq__() 매직 매서드가 필요한 이유는 bfs 너비 우선 탐색에서 explored: Set 로 이미 방문한 곳인지 확인하게 된다. 선교사 문제의 successors() 함수에서 새로운 상태의 MCState클래스로 반환할 때 클래스 내부의 상태가 같다면 같은 개체로 인정한다는 동등성을 만들어줘야 한다. 즉 서로 다른 개체가 동등함을 보이기 위해 매직 매서드를 작성해야된다.
참고문헌

고전 알고리즘 인 파이썬
Leave a comment