[Algorithm] 제약 충족 문제

15 minute read

고전 알고리즘 인 파이썬

제약 충족 문제

광범위한 제약 충족 문제 해결의 기초

변수
도메인 : 변수들이 가지는 범위
제약 조건

간단한 재귀 백트래킹 검색을 사용하여 제약 충족 문제를 해결하는 방법

백트래킹이란 앞장에서 본 DFS(깊이 우선 탐색)과 같이 탐색 중 벽에 막혔을 때, 마지막 지점으로 돌아가 다른 경로를 선택하는 방안이다.

3.1 제약 충족 문제 프레임워크

Constraint 클래스 : 제약 조건 변수와 이를 충족하는지 검사하는 메서드(satisfied())로 구성
추상 클래스로 정의하여 기본 구현을 override한다.

# csp.py
from typing import Generic, TypeVar, Dict, List, Optional
from abc import ABC, abstractmethod

V = TypeVar('V') # 변수 타입
D = TypeVar('D') # 도메인 타입

# 제약 조건
class Constraint(Generic[V, D], ABC):
    # 제약 조건 변수
    def __init__(self, variables: List[V]) -> None:
        self.variables = variables
        
    # 서브클래스 메서드에서 오버라이드
    @abstractmethod
    def satisfied(self, assignment: Dict[V, D]) -> bool:
        pass

NOTE: 추상 클래스는 메서드의 목록만 가진 클래스이며 상속받는 파생 클래스에서 메서드를 구현을 강제하기 위해 사용한다. 추상 클래스의 추상 메서드를 구현했지는 파생 클래스가 인스턴스를 만들 때 확인한다.

CSP 클래스 : 변수, 도메인, 제약조건 저장

# csp.py
...
class CSP(Generic[V, D]):
    def __init__(self, variables: List[V], domains: Dict[V, List[D]]) -> None:
        self.variables: List[V] = variables # 제약조건을 확인할 변수
        self.domains: Dict[V, List[D]] = domains # 각 변수의 도메인
        self.constraints: Dict[V, List[Constraint[V, D]]] = {}
            
        for variable in self.variables:
            self.constraints[variable] = []
            if variable not in self.domains:
                raise LookupError("모든 변수에 도메인이 할당되어야 합니다.")
        
    def add_constraint(self, constraint: Constraint[V, D]) -> None:
        for variable in constraint.variables:
            if variable not in self.variables:
                raise LookupError("제약 조건 변수가 아닙니다.")
            else:
                self.constraints[variable].append(constraint)
    
    # 주어진 변수의 모든 제약 조건을 만족하는 지 검사
    def consistent(self, variable:V, assignment: Dict[V, D]) -> bool:
        for constraint in self.constraints[variable]:
            if not constraint.satisfied(assignment):
                return False
        return True
    
    def backtracking_search(self, assignment: Dict[V, D] = {}) -> Optional[Dict[V, D]]:
        # assignment는 모든 변수가 할당될 때 완료된다. => 기저조건
        if len(assignment) == len(self.variables):
            # 모든 변수의 유효할당을 찾았음으로 탐색종료
            return assignment         
        
        # 할당되지 않은 모든 변수
        unassigned: List[V] = [v for v in self.variables if v not in assignment]
            
        # 할당되지 않은 첫 번째 변수의 가능한 모든 도메인 값을 가져온다.
        first: V = unassigned[0]
        for value in self.domains[first]:
            local_assignment = assignment.copy()
            local_assignment[first] = value
            # local_assignment 값이 일관적이면 재귀호출
            if self.consistent(first, local_assignment):
                result: Optional[Dict[V, D]] = self.backtracking_search(local_assignment)
            # 결과를 찾지 못하면 백트래킹 종료
                if result is not None:
                    return result
        return None # 솔루션 없음

__init__() 메서드에서 제약조건을 Dict 타입의 self.constraints 변수를 생성한다.
add_constraint() 메서드에서 모든 변수에 대해 제약 조건을 확인하고, 각 제약 조건 매핑에 자신을 추가한다.
주어진 변수 구성을 assignment(할당)이라고 하며, consistent() 메서드는 주어진 변수와 선택된 도메인값이 제약조건을 충족시키는지 확인한다.
backtracking_search() 메서드에서 구현된 백트래킹은 재귀 깊이 우선 탐색의 일종이다.
backtracking_search() 의 기저조건은 모든 변수에 대한 유효한 할당을 찾는 것이다. 즉 할당된 변수와 변수들의 길이가 같을 경우이다.

모든 변수가 할당되지 않았을 경우

unassigned 변수에 할당이 되지않은 List를 구성하고 첫 번째 항목을 first 변수에 할당한다.
first 변수에 가능한 모든 도메인 값을 local_assignment에 Dict형태로 저장한다.
local_assignment 변수의 새 할당이 모든 제약을 만족하면(self.consistent() 사용) 새 할당을 제자리에서 재귀적으로 검색한다.
특정 변수에서 가능한 모든 도메인값을 확인했을 때 솔루션이 없다면 None을 반환하고, 이전 재귀 체인으로 돌아간다.(백트랙킹)

3.2 지도 색칠 문제

출처: 호주지도 무료이미지

호주의 지도를 아래의 제약을 만족하며 색을 칠 할 것이다.

모델링

변수 : 호주의 7개 지역 (뉴사우스웨일스, 빅토리아, 퀸즐랜드, 사우스 오스트레일리아, 웨스턴 오스트레일리아, 태즈메이니아, 노던 준주)
도메인 : 3가지 색상 (빨강, 파랑, 녹색)
제약 : 인접한 두 지역을 같은 색상을 할당할 수 없다.

제약조건은 이진 제약 조건(두 변수 사이의 제약 조건)을 사용한다.
Constraint 베이스 클래스를 상속하는 MapColoringConstraint 서브클래스를 구현한다.

오버라이드된 satisfied() 메서드는 할당된 도메인이 있는지 확인한 후, 둘 중 하나라도 색상이 없다면 색상이 지정되지 전까지 제약조건을 만족한다. 이후 두 지역의 색상이 다른지 확인한다.

#map_coloring.py
from csp import Constraint, CSP
from typing import Dict, List, Optional

class MapColoringConstraint(Constraint[str, str]):
    def __init__(self, place1: str, place2: str) -> None:
        super().__init__([place1, place2])
        self.place1: str = place1
        self.place2: str = place2
            
    def satisfied(self, assignment: Dict[str, str]) -> bool:
        # 두 지역 중 하나가 색상이 할당되지 않은 경우 충돌은 발생하지 않는다.
        if self.place1 not in assignment or self.place2 not in assignment:
            return True
        # place1과 2에 할당된 색상이 다른지 확인한다.
        return assignment[self.place1] != assignment[self.place2]

TIP: 위 코드의 super().__init__([place1, place2]) 부분에 Constraint.__init__([place1, place2]) 처럼 클래스 이름을 사용할 수도 있다. 다중 상속을 처리하는 경우 어떤 슈퍼클래스를 호출하는지 명시적으로 알 수 있기 때문에 유용하다.

지역 간 제약 조건을 확인하는 방법을 구현했으므로 CSP클래스를 사용하여 변수와 도메인, 제약조건을 추가한다.

#map_coloring.py
variables: List[str] = ["뉴사우스웨일스", "빅토리아", "퀸즐랜드", "사우스 오스트레일리아",
                        "웨스턴 오스트레일리아", "태즈메이니아", "노던 준주"]
domains: Dict[str, List[str]] = {}

for variable in variables:
    domains[variable] = ["빨강", "초록", "파랑"]

csp: CSP[str, str] = CSP(variables, domains)
csp.add_constraint(MapColoringConstraint("웨스턴 오스트레일리아", "노던 준주"))
csp.add_constraint(MapColoringConstraint("웨스턴 오스트레일리아", "사우스 오스트레일리아"))
csp.add_constraint(MapColoringConstraint("사우스 오스트레일리아", "노던 준주"))
csp.add_constraint(MapColoringConstraint("퀸즐랜드", "노던 준주"))
csp.add_constraint(MapColoringConstraint("퀸즐랜드", "뉴사우스웨일스"))
csp.add_constraint(MapColoringConstraint("뉴사우스웨일스", "사우스 오스트레일리아"))
csp.add_constraint(MapColoringConstraint("빅토리아", "사우스 오스트레일리아"))
csp.add_constraint(MapColoringConstraint("빅토리아", "뉴사우스웨일스"))
csp.add_constraint(MapColoringConstraint("빅토리아", "태즈메이니아"))

# backtracking_search() 메서드를 호출하여 호주 지도를 색칠한다.
solution: Optional[Dict[str, str]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    print(solution)

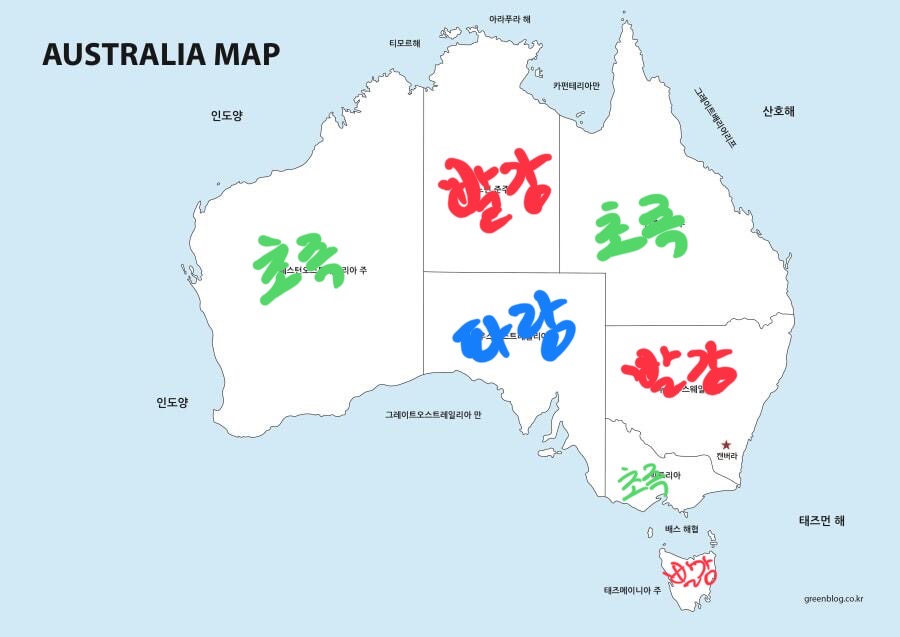
{'뉴사우스웨일스': '빨강', '빅토리아': '초록', '퀸즐랜드': '초록', '사우스 오스트레일리아': '파랑', '웨스턴 오스트레일리아': '초록', '태즈메이니아': '빨강', '노던 준주': '빨강'}

지도색칠문제

3.3 여덟 퀸 문제

8 X 8 격자로 되어 있는 체스보드에서 퀸은 체스보드의 모든 행과 열, 대각선으로 이동가능할 때, 한 퀸의 이동영역에 다른 퀸이 존재하지 않도록 여덟개의 퀸을 배치하는 것이다.

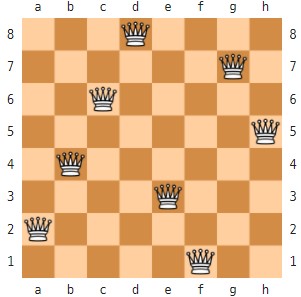
여덟 퀸 문제-출처 위키백과

출처 위키백과

모델링

변수 : 퀸의 열 (1, 2, 3, 4, 5, 6, 7, 8)
도메인 : 체스보드의 행(1, 2, 3, 4, 5, 6, 7, 8)
제약 : 퀸의 이동영역에 다른 퀸을 놓을 수 없다.

# queens.py
columns: List[int] = [1,2,3,4,5,6,7,8]
rows: Dict[int, List[int]] = {}
for column in columns:
    rows[column] = [1,2,3,4,5,6,7,8]
csp:CSP[int, int] = CSP(columns, rows)

제약 조건 중 다른 두 퀸이 대각선에 존재한다면 두 퀸의 행 차이와 열 차이는 같다 는 것을 이용하여 QueensConstraint 클래스를 구현한다.

#queens.py
from csp import Constraint, CSP
from typing import Dict, List, Optional

class QueensConstraint(Constraint[int, int]):
    def __init__(self, columns: List[int]) -> None:
        super().__init__(columns)
        self.columns: List[int] = columns
    
    def satisfied(self, assignment: Dict[int, int]) -> bool:
        # q1c = 퀸1 열, q1r = 퀸1 행
        for q1c, q1r in assignment.items():
            # q2c = 퀸2 열
            for q2c in range(q1c + 1, len(self.columns) + 1):
                if q2c in assignment:
                    q2r: int = assignment[q2c] # q2r = 퀸 2 행
                    if q1r == q2r: # 같은 열에 존재하는가
                        return False
                    if abs(q1r - q2r) == abs(q1c - q2c): # 대각선에 존재하는가
                        return False
        return True

csp.add_constraint(QueensConstraint(columns))
solution: Optional[Dict[int, int]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    print(solution)

{1: 1, 2: 5, 3: 8, 4: 6, 5: 3, 6: 7, 7: 2, 8: 4}

3.4 단어 검색

단어 검색은 격자에서 행과 열, 대각선을 따라 배치된 특정 단어를 찾는 문제이다. 찾으려는 단어를 격자에 배치하는 것은 일종의 제약 충족 문제이다.

모델링

변수 : 5가지의 단어 (“MATTHEW”, “JOE”, “MARY”, “SARAH”, “SALLY”)
도메인 : 격자 안에 들어갈 수 있는 위치
제약 : 단어의 위치가 중복될 수 없다.

# word_search.py
from typing import NamedTuple, List, Dict, Optional
from random import choice
from string import ascii_uppercase
from csp import CSP, Constraint

Grid = List[List[str]] # 격자 타입 앨리어스

class GridLocation(NamedTuple):
    row: int
    column: int
        
def generate_grid(rows:int, columns: int) -> Grid:
    # 임의의 문자로 격자를 초기화
    return [[choice(ascii_uppercase) for c in range(columns)] for r in range(rows)]

def display_grid(grid: Grid) -> None:
    for row in grid:
        print(" ".join(row))
        
def generate_domain(word: str, grid: Grid) -> List[List[GridLocation]]:
    domain: List[List[GridLocation]] = []
    height: int = len(grid)
    width: int = len(grid[0])
    length: int = len(word)
    for row in range(height):
        for col in range(width):
            columns: range = range(col, col + length + 1)
            rows: range = range(row, row + length + 1)
            if col + length <= width:
                # 왼쪽에서 오른쪽으로 단어 배치
                domain.append([GridLocation(row, c) for c in columns])
                # 대각선 오른쪽 아래로 배치
                if row + length <= height:
                    domain.append([GridLocation(r, col + (r - row)) for r in rows])
            if row + length <= height:
                # 위에서 아래로
                domain.append([GridLocation(r, col) for r in rows])
                # 대각선 왼쪽 아래로
                if col - length >= 0:
                    domain.append([GridLocation(r, col - (r - row)) for r in rows])
    return domain

generate_grid() 메서드를 통해 영문자로 격자를 채운다.
특정 단어가 격자에 들어갈 수 있는 위치를 파악하기 위해 generate_domain() 메서드를 구현한다.
generate_domain() 메서드는 모든 단어에 대해 왼쪽 위부터 오른쪽 아래까지 모든 격자 위치를 순회하기 때문에 많은 연산이 필요하다.

# word_search.py
class WordSearchConstraint(Constraint[str, List[GridLocation]]):
    def __init__(self, words: List[str]) -> None:
        super().__init__(words)
        self.words: List[str] = words
    
    def satisfied(self, assignment: Dict[str, List[GridLocation]]) -> bool:
        # 중복된 격자 위치가 있다면 그 위치는 곂치는 부분임.
        all_locations = [locs for values in assignment.values() for locs in values]
        return len(set(all_locations)) == len(all_locations)

단어의 위치 범위가 맞는지 확인하기 위해 단어 검색 제약 조건을 구현한다.

satisfied() 메서드는 한 단어의 위치가 격자에 있는 다른 단어의 위치와 동일한지 여부를 확인한다.

Set 자료형을 사용하는 이유는 중복을 허용하지 않기 때문에 원본 리스트의 항목 수보다 셋으로 변환된 항목 수가 작으면 리스트에 일부 중복된 항목이 있다는 것을 의미한다.

9 X 9 격자에 5개의 단어를 넣는 코드이다.

# word_search.py
grid: Grid = generate_grid(9, 9)
words: List[str] = ["MATTHEW", "JOE", "MARY", "SARAH", "SALLY"]
locations: Dict[str, List[GridLocation]] = {}
for word in words:
    locations[word] = generate_domain(word, grid)
csp: CSP[str, List[GridLocation]] = CSP(words, locations)
csp.add_constraint(WordSearchConstraint(words))

solution: Optional[Dict[str, List[GridLocation]]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    for word, grid_locations in solution.items():
        # 50% 확률로 grid_locations를 반전한다.
        if choice([True, False]):
            grid_locations.reverse()
        for index, letter in enumerate(word):
            (row, col) = (grid_locations[index].row, grid_locations[index].column)
            grid[row][col] = letter
    display_grid(grid)

M A T T H E W R T
M A R Y F S S R E
C M C F T A Y C O
Z A I U Q R L B J
E E W B H A L Q C
B K V A Q H A M R
W O M A J L S S T
H U G D T T T I S
J S A D C I I R O

3.5 SEND+MORE=MONEY

NOTICE: 복면산 퍼즐이란 계산식에서 숫자를 문자나 그림 등으로 가려놓고 어떤 숫자가 들어가는지 알아맞히는 퍼즐이다. 숫자가 마치 복면을 쓰고 있는 것 같다고 하여 복면산이라고 부른다.

모델링

변수 : 8개의 문자 (“S”,”E”,”N”,”D”,”M”,”O”,”R”,”Y”)
도메인 : 한 자리 숫자 (0~9)
제약 조건 : 숫자는 중복될 수 없으며, SEND+MORE=MONEY를 만족

from csp import Constraint, CSP
from typing import Dict, List, Optional

class SendMoreMoneyConstraint(Constraint[str, int]):
    def __init__(self, letters: List[str]) -> None:
        super().__init__(letters)
        self.letters: List[str] = letters
            
    def satisfied(self, assignment: Dict[str, int]) -> bool:
        # 할당된 숫자가 중복인가
        if len(set(assignment.values())) < len(assignment):
            return False
        
        # 모든 변수에 숫자를 할당해서 계산이 맞는지 확인한다.
        if len(assignment) == len(self.letters):
            s: int = assignment["S"]
            e: int = assignment["E"]
            n: int = assignment["N"]            
            d: int = assignment["D"]            
            m: int = assignment["M"]            
            o: int = assignment["O"]            
            r: int = assignment["R"]            
            y: int = assignment["Y"]            
            send: int = s * 1000 + e * 100 + n * 10 + d
            more: int = m * 1000 + o * 100 + r * 10 + e
            money: int = m * 10000 + o * 1000 + n * 100 + e * 10 + y
            return send + more == money
        return True # 충돌 없음

SendMoreMoneyConstraint 클래스에서는 두가지를 확인한다.

할당된 숫자가 중복인가
모든 글자에 숫자가 할당됬다면, SEND+MORE=MONEY 수식을 만족하는가

letters: List[str] = ["S","E","N","D","M","O","R","Y"]
possible_digits: Dict[str, List[int]] = {}

for letter in letters:
    possible_digits[letter] = [0,1,2,3,4,5,6,7,8,9]

possible_digits["M"] = [1] # 만의 자릿 수는 0이 아니다.
csp: CSP[str, int] = CSP(letters, possible_digits)
csp.add_constraint(SendMoreMoneyConstraint(letters))

solution: Optional[Dict[str, int]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    print(solution)

{'S': 9, 'E': 5, 'N': 6, 'D': 7, 'M': 1, 'O': 0, 'R': 8, 'Y': 2}

SEND+MORE=MONEY » 9567 + 1085 = 10652

3.6 회로판 레이아웃

사각형 회로판에 특정 칩을 장착하는 경우, 다양한 사각형 모양의 칩을 장착하는 제약 충족 문제이다.

모델링

변수 : $M \times N$ 사각형의 칩
도메인 : $9 \times 9$ 격자에 들어갈 수 있는 곳
제약 조건: 사각형은 서로 겹칠 수 없다.

# 회로판 레이아웃
from typing import NamedTuple, List, Dict, Optional
from csp import CSP, Constraint

Grid = List[List[str]] # 격자 타입 앨리어스

class GridLocation(NamedTuple):
    row: int
    column: int

def generate_grid(rows:int, columns: int) -> Grid:
    # *로 격자를 초기화
    return [["*" for c in range(columns)] for r in range(rows)]

def display_grid(grid: Grid) -> None:
    for row in grid:
        print(" ".join(row))

def generate_domain(board: int, grid: Grid) -> List[List[GridLocation]]:
    domain: List[List[GridLocation]] = []
    height: int = len(grid)
    width: int = len(grid[0])
    board_height: int = board // 10 # 회로의 높이
    board_width: int = board % 10 # 회로의 넓이
    for row in range(height):
        for col in range(width):
            columns: range = range(col, col + board_width)
            rows: range = range(row, row + board_height)
            if col + board_width <= width and row + board_height <= height:
                # 격자 내에 할당될 수 있는 위치
                domain.append([GridLocation(r, c) for r in rows for c in columns])
    return domain

3.4 단어검색 의 코드를 변형하여 회로판 레이아웃을 해결한다.

generate_domain() 함수는 도메인을 생성하는 함수로 int 자료형의 형태로 넘어온 변수 ( ex 61: $6\times 1$ ) 를 통해 회로의 높이와 넓이를 구한다.

격자의 가로와 세로의 크기를 넘지 않는 범위를 도메인 List에 append하여 반환한다.

class BoardSearchConstraint(Constraint[int, List[GridLocation]]):
    def __init__(self, boards: List[int]) -> None:
        super().__init__(boards)
        self.boards: List[int] = boards
    
    def satisfied(self, assignment: Dict[int, List[GridLocation]]) -> bool:
        all_locations = [locs for values in assignment.values() for locs in values ]
        return len(set(all_locations)) == len(all_locations)

satisfied() 메서드는 문자검색과 동일하게 위치가 중복되지 않는 제약을 만족해야 한다.

fill_board: Dict = {61: "1", 44: "2", 33: "3", 22: "4", 25: "5"}

grid: Grid = generate_grid(9,9)
boards: List[int] = [61, 44, 33, 22, 25]
locations: Dict[int, List[GridLocation]] = {}

for board in boards:
    locations[board] = generate_domain(board, grid)

csp: CSP[int, List[GridLocation]] = CSP(boards, locations)
csp.add_constraint(BoardSearchConstraint(boards))

solution: Optional[Dict[str, List[GridLocation]]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    for board, grid_locations in solution.items():
        for index in range((board // 10) * (board % 10)):
            (row, col) = (grid_locations[index].row, grid_locations[index].column)
            grid[row][col] = fill_board[board]
    display_grid(grid)

1 2 2 2 2 3 3 3 *
1 2 2 2 2 3 3 3 *
1 2 2 2 2 3 3 3 *
1 2 2 2 2 4 4 * *
1 * * * * 4 4 * *
1 5 5 5 5 5 * * *
* 5 5 5 5 5 * * *
* * * * * * * * *
* * * * * * * * *

fill_board 는 출력을 보기 편하게 하기 위해 Dict로 변수와 str자료형으로 선언한 후 solution을 구해 출력한다.

연습문제

1번

WordSearchConstraint 클래스를 수정하여 중복 단어를 허용하는 단어 검색을 구현하라.

모델링

변수 : 5가지의 단어 (“MATTHEW”, “JOE”, “MARY”, “SARAH”, “SALLY”)
도메인 : 격자 안에 들어갈 수 있는 위치
제약 : 단어의 위치가 하나만 중복 될 수 있다.

# word_search.py
...
class WordSearchConstraint(Constraint[str, List[GridLocation]]):
    def __init__(self, words: List[str]) -> None:
        super().__init__(words)
        self.words: List[str] = words
    
    def satisfied(self, assignment: Dict[str, List[GridLocation]]) -> bool:
        board = [["" for c in range(9)] for r in range(9)]
        for word, locations in assignment.items():
            for i in range(len(word)):
                if board[locations[i].row][locations[i].column] != "" and \
                board[locations[i].row][locations[i].column] != word[i]:
                        return False
                else:
                    board[locations[i].row][locations[i].column] = word[i]
        return True

제약 조건: 중복을 허용하지 않는다. » 각 단어의 한자리씩 곂칠 수 있다. (직선으로 할당되면, 단어가 곂치는 부분은 서로 한개 이상 있을 수 없기 때문에)

satisfied() 함수 내에서 보드를 만들어 단어를 할당시킬 때, board에 다른 단어가 있으면 False를 반환했다.
메모리를 낭비하기 때문에 더 좋은 방법이 있나 찾아봐야겠다.

# word_search.py
grid: Grid = generate_grid(9, 9)
words: List[str] = ["MATTHEW", "JOE", "MARY", "SARAH", "SALLY"]
locations: Dict[str, List[GridLocation]] = {}
for word in words:
    locations[word] = generate_domain(word, grid)
csp: CSP[str, List[GridLocation]] = CSP(words, locations)
csp.add_constraint(WordSearchConstraint(words))

solution: Optional[Dict[str, List[GridLocation]]] = csp.backtracking_search()
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    for word, grid_locations in solution.items():
        for index, letter in enumerate(word):
            (row, col) = (grid_locations[index].row, grid_locations[index].column)
            grid[row][col] = letter
    display_grid(grid)

M A T T H E W U P
S A L L Y E N E H
T J R X U K L O A
K Y S Y Z B D J R
Y K G C T E O O A
Q L Q H O V H F S
D N J D N Q B S P
J Z I T G P Q L U
Y U S S T F U R I

2번

제약 충족 문제 해결 프레임워크를 이용하여 스도쿠 문제를 해결할 수 있는 프로그램을 작성하라.

모델링

변수 : $9 \times 9$ 의 그리드 중 빈 그리드
도메인이 : 1 ~ 9 까지의 수
제약: 가로, 세로, $3 \times 3$ 9칸에 중복되는 수가 없어야 한다.

from typing import NamedTuple, List, Dict, Optional
from csp import CSP, Constraint

Grid = List[List[str]] # 격자 타입 앨리어스

class GridLocation(NamedTuple):
    row: int
    column: int

def display_grid(grid: Grid) -> None:
    for row in grid:
        print(row)

# board에서 빈 칸을 찾는 함수
def find_empty(board: Grid) -> List[GridLocation]:
    variables: List[GridLocation] = []
    for i in range(len(board)):
        for j in range(len(board)):
            if board[i][j] == 0:
                variables.append(GridLocation(i,j))  # row, col
    return variables

class SudokuSearchConstraint(Constraint[GridLocation, int]):
    def __init__(self, grid_locations: List[GridLocation]) -> None:
        super().__init__(grid_locations)
        self.grid_locations: List[GridLocation] = grid_locations
            
    def satisfied(self, assignment: Dict[GridLocation, int]):
        for loc, num in assignment.items():
            # 가로확인
            for x in range(9):
                if board[loc.row][x] == num and x != loc.column:
                    board[loc.row][loc.column] = 0
                    return False
            # 세로확인
            for y in range(9):
                if board[y][loc.column] == num and y != loc.row:
                    board[loc.row][loc.column] = 0
                    return False
            # 3 * 3 확인
            startRow = loc.row - (loc.row % 3)
            startCol = loc.column - (loc.column % 3)
            for i in range(startRow, startRow + 3):
                for j in range(startCol, startCol + 3):
                    if board[i][j] == num and GridLocation(i,j) != loc:
                        board[loc.row][loc.column] = 0
                        return False
        for loc, num in assignment.items():
            board[loc.row][loc.column] = num
        return True

find_empty() 함수는 변수를 구하기 위해 board 에서 0인 GridLocation 을 반환한다.
SudokuSearchConstraint() 의 satisfied() 메서드는 제약 조건 가로, 세로, $3 \times 3$ 의 9 그리드의 중복되는 숫자가 없음을 찾는다.

board: Grid = [
    [7,8,0,4,0,0,1,2,0],
    [6,0,0,0,7,5,0,0,9],
    [0,0,0,6,0,1,0,7,8],
    [0,0,7,0,4,0,2,6,0],
    [0,0,1,0,5,0,9,3,0],
    [9,0,4,0,6,0,0,0,5],
    [0,7,0,3,0,0,0,1,2],
    [1,2,0,0,0,7,4,0,0],
    [0,4,9,2,0,6,0,0,7]
]
variables: List[GridLocation] = find_empty(board) # 변수
domains: Dict[GridLocation, List[int]] = {} # 도메인
for variable in variables:
    domains[variable] = [1,2,3,4,5,6,7,8,9]

csp: CSP[GridLocation, List[int]] = CSP(variables, domains)
csp.add_constraint(SudokuSearchConstraint(variables))

solution: Optional[Dict[Grid, int]] = csp.backtracking_search()
    
if solution is None:
    print("답을 찾을 수 없습니다.")
else:
    for loc, num in solution.items():
        board[loc.row][loc.column] = num
    display_grid(board)

[7, 8, 5, 4, 3, 9, 1, 2, 6]
[6, 1, 2, 8, 7, 5, 3, 4, 9]
[4, 9, 3, 6, 2, 1, 5, 7, 8]
[8, 5, 7, 9, 4, 3, 2, 6, 1]
[2, 6, 1, 7, 5, 8, 9, 3, 4]
[9, 3, 4, 1, 6, 2, 7, 8, 5]
[5, 7, 8, 3, 9, 4, 6, 1, 2]
[1, 2, 6, 5, 8, 7, 4, 9, 3]
[3, 4, 9, 2, 1, 6, 8, 5, 7]

Share on

Twitter Facebook LinkedIn

[Algorithm] 제약 충족 문제

고전 알고리즘 인 파이썬

목차

제약 충족 문제

3.1 제약 충족 문제 프레임워크

3.2 지도 색칠 문제

3.3 여덟 퀸 문제

3.4 단어 검색

3.5 SEND+MORE=MONEY

3.6 회로판 레이아웃

연습문제

1번

2번

Share on

Leave a comment

You may also enjoy

[MachineLearning] Flask web app 만들기

[MachineLearning] 요리지역분류(3)

[MachineLearning] 요리지역분류(2)

[MachineLearning] 요리지역분류(1)